Zde má být fotka! Asi není nastaveno vykreslování obrázků.    Konzultace v ZS 2022:
Žižkova 17, areál FAST
pracovna Z 213

každý pátek
  9:30 – 10:00
12:00 – 12:30 		   Zde má být logo! Asi není nastaveno vykreslování obrázků.

Materiály z matematiky a deskriptivní geometrie pro samostatné studium

Středoškolská matematika

BAA015 – Deskriptivní geometrie (APS)

BAA001 – Matematika 1

BAA012 – Matematika 1 (EVB)

BAA002 – Matematika 2

BAA003 – Matematika 3

BAA010 – Matematika 3 (G)

Zpět
             Zde má být titulní strana učebnice! Asi není nastaveno vykreslování obrázků.

Harmonogram cvičení od 19. září 2022

  1. Kuželosečky: Apolloniova definice kuželoseček,
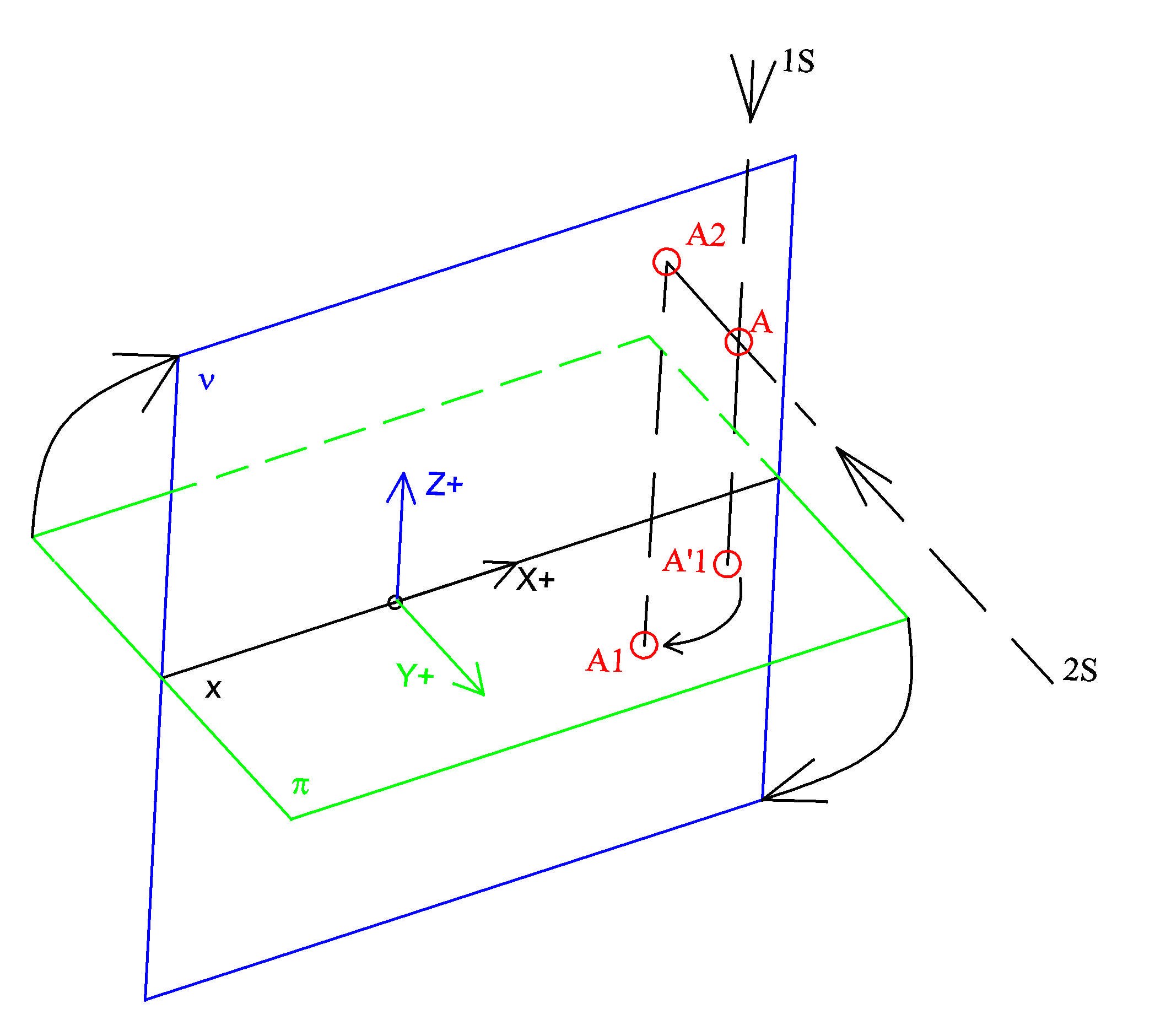
 2. Mongeovo promítání    půdorysna π (zelená, osy x,y); nárysna ν (modrá, osy x,z) – video FAST
(Soubor CD-ROMů Deskriptivní geometrie / pro I. ročník Stavební fakulty VUT v Brně / Kap. 5. Mongeova projekce [čti monžova]) 		Asi není nastaveno vykreslování obrázků!
  • Zobrazení bodu
    • (CD př. 5. 1. / obr. 5. 5.) V Mongeově projekci dané základnicí x12 s počátkem O vyneste body, přičemž A=[–15; 23; 45], B=[20; –38; 17].
  • Zobrazení přímky
    • (CD př. 5. 2. / obr. 5. 8.) Přímka m je dána svými sdruženými průměty m1, m2 (obr. 5. 8.). Nalezněte její stopníky.
    • (CD př. 5. 3. / obr. 5. 12.) Jsou dány přímka k a bod M svými sdruženými průměty (obr. 5. 12.). Bodem M veďte libovolnou různoběžku s přímkou k.
  • Zobrazení roviny
    • (CD př. 5. 4. / obr. 5. 15.) Rovina ρ je dána bodem A a přímkou a, která bodem A neprochází (obr. 5. 15.). K danému půdorysu M1 bodu M sestrojte nárys M2 tak, aby bod M ležel v rovině ρ.
    • (CD př. 5. 5. / obr. 5. 18.) Sestrojte stopy roviny ρ=(–20; –42; 15).
    • (CD př. 5. 6. / obr. 5. 21.) Je dána rovina ρ=(20; -40; 15) a bod M=[–10; 35; ?], který v rovině ρ leží. Sestrojte nárys bodu M.
    • (CD př. 5. 7. / obr. 5. 23.) Rovina ρ je dána bodem C=[15; 30; 40] a přímkou a=(AB), kde A=[-35; 35; 7], B=[–10; 23; 18]. Sestrojte stopy roviny ρ.
  • Vzdálenost bodu od roviny
    • (CD př. 5. 11. / obr. 5. 46.) Určete vzdálenost bodu M=[15; 40; 30] od roviny α=(25; 10; –35).
  • Vzdálenost bodu od přímky
    • (CD př. 5. 16a) Určete vzdálenost bodu M=[45; 40; 20] od přímky m(P=[25; 5; 45], Q[0; 50; 30]) pomocí roviny jdoucí bodem M kolmo k přímce m.
    • bod a přímka určují rovinu (bod i přímku si volte libovolně podobně jako v odkazu)
  • Vzdálenost dvou rovnoběžných rovin
    • (CD př. 5. 16b) Určete vzdálenost dvou rovnoběžných rovin α=(–40; 45; 30) a β=(–10; ?; ?).
    • (CD př. 5. 19. / obr. 5. 59. — užitím třetí průmětny) stopy rovin si volte libovolně.
  • Zobrazení kružnice v obecné rovině
    • (CD př. 5. 14. / obr. 5. 53.) Sestrojte průměty kružnice k(S=[20; 30; ?], r=25), která leží v rovině ro=(–40; 40; 30).
    • (CD př. 5. 15. / obr. 5. 54.) Sestrojte průměty kružnice k(S=[20; 30; ?], r=25), která leží v rovině ro=(–40; 40; 30).
    • (CD př. 5. 16. / obr. 5. 55.) Obraz kružnice opsané trojúhelníku ΔABC, kde A=[10; 30; 20], B=[–20; 45; 35], C=[0; 10; 50].
  3. Mongeovo promítání    Jehlan, rotační válec    (STŘEDOVÁ KOLINEACE A OSOVÁ AFINITA).
  • Pravidelný čtyřboký jehlan (rozbor) s podstavou v α: α(–60;60;70), A[25;?;70], S[10;30;?], v=60 (konstrukce).
  • Rotační válec (rozbor): o=(P[–40;15;0], Q[30;100;100]), M[–20;60;15] leží na kružnici spodní podstavy, v=80 (část konstrukce).
  4. Mongeovo promítání    Řez hranolu a jehlanu. Průnik přímky s hranolem, jehlanem, válcem, kuželem. Řez šikmého válce (CD př. 5. 31. / obr. 5. 80.). (postup).
Vytiskněte si zadání!

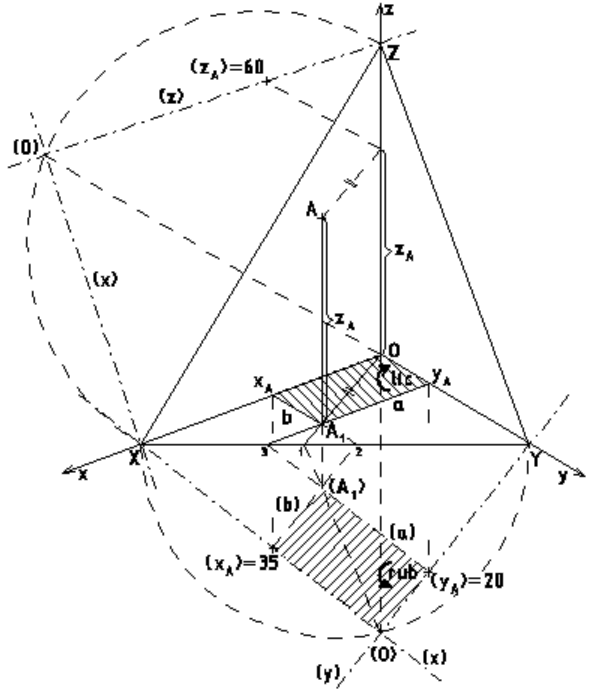
  5.
Kolmá axonometrie
  • Zobrazení bodu: ΔXYZ(90;100;110), A[35;20;60]
  • Zobrazení roviny (CD př. 6. 7. / obr. 6. 25.) Axonometrie je určena ΔXYZ. Sestrojte stopy rovin α=(50;90;70), β=(–50;90;70).
  • Stopníky přímky
    • (CD cvičení 6. 5. 1.) Zobrazte přímku p(A,B) a její stopníky, je-li dáno: ΔXYZ(100;110;120), A=[55;30;40], B=[25;50;75].
    • (CD cvičení 6. 5. 5.) Přímka p(A,B) protíná osu y. Určete B1, p2, p3.
    • (CD cvičení 6. 5. 6.) Určete p1, p2, p3, je-li dána přímka p(A,O).
  • Průsečnice dvou rovin (CD cvičení 6. 7. 2.)
  • Průsečík přímky s rovinou. (CD př. 6. 2. / obr. 6. 38.) Sestrojte průsečík přímky dané axonometrickým "průmětem" a "půdorysem" s rovinou α zadanou stopami.
  • Kružnice v půdorysně
  • Kružnice v bokorysně, která se dotýká půdorysny π: ΔXYZ(110;120;100), S=[0;40;30].
    • Lze využít CD př. 6. 18. / obr. 6. 43. (nebo př. 6. 19. / obr. 6. 44.)
Asi není nastaveno vykreslování obrázků!
  6. Kolmá axonometrie (tělesa mají podstavu v půdorysně)
 
Vytiskněte si zadání!

Řez šikmého čtyřbokého hranolu, pravidelného šestibokého hranolu, pravidelného čtyřbokého jehlanu a pravidelného pětibokého jehlanu.
Průnik přímky se šikmým čtyřbokým hranolem, pravidelným čtyřbokým jehlanem, šikmým kruhovým válcem a rotačním kuželem.
Řez rotačního válce s podstavou v půdorysně π (zadání bez souřadnic).
 
Další příklady ve formátu PDF
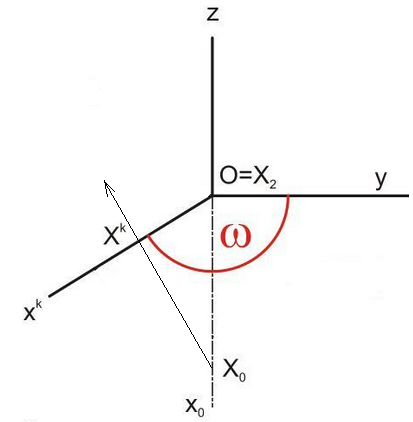
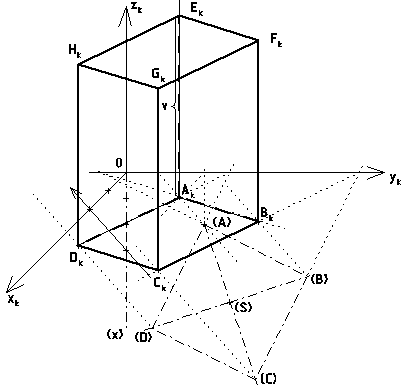
  7. Kosoúhlé promítání     ω označuje úhel průmětů souřadnicových os x a y; zkracuje se osa x. Směr zkrácení je současně směr afinity mezi kosoúhlými půdorysy a jejich otočenými obrazy, při otočení půdorysny π kolem osy y (která je osou afinity) do průmětny μ(y,z).
  • Kružnice v půdorysně π: ω=120°, q=4/5, S[50;78;0], M[75;100;0].
  • Průnik přímky q=(P[–10;110;0], Q[70;30;50]) s pravidelným čtyřbokým jehlanem s podstavou v půdorysně π: ω=135°, q=3/4, A[80;65;0], S[50;60;0], v=100.
  • Řezy těles
Asi není nastaveno vykreslování obrázků! Asi není nastaveno vykreslování obrázků! Asi není nastaveno vykreslování obrázků!
  8. Lineární perspektiva je středové promítání, které se snaží napodobit lidské oko. … V technické praxi se využívá především k zobrazování objektů větších rozměrů. Perspektivními obrazy jsou například fotografie.
  • Úlohy v základní rovině
    • úběžníky (úběžník=průmět nevlastního bodu přímky)
      • CD př. 7. 9. / obr. 7. 45. (třetinový úběžník)
      • rovnoběžka k přímce a bodem B při poloviční distanci (bod i přímka leží v základní rovině)
      • CD př. 7. 2. / obr. 7. 30. (vynášení výšek od základní roviny)
      • CD př. 7. 4. / obr. 7. 33. (hloubkové a průčelné přímky)
      • hranol stojící na základní rovině
    • měřící body (úběžník směru, kterým se úsečka AB v základní rovině promítá do stejně dlouhé úsečky A'B' na základnici z)
      • CD př. 7. 5. / obr. 7. 36. (měřící bod a jeho použití)
      • CD př. 7. 7. / obr. 7. 41. (trojúhelník v základní rovině)
      • čtvercová síť v základní rovině
      • dva čtverce v základní rovině (poloviční distance => poloviční měřící bod)
    • sklopený půdorys
      • CD př. 7. 15. / obr. 7. 53.a) (kolmá přímka, obě v základní rovině)
      • CD př. 7. 15. / obr. 7. 53.b) (totéž v poloviční distanci)
      • CD př. 7. 16. / obr. 7. 54. (úhel přímek, obě v základní rovině)
      • PDF   (trojúhelník v základní rovině)
      • CD obr. 7. 64. (sklopení přímky ležící v základní rovině)
      • CD obr. 7. 66. (sklopení obecného bodu pomocí hloubkové přímky)
      • CD př. 7. 20. / obr. 7. 67. (perspektivní půdorys ze sklopeného půdorysu)
      • CD př. 7. 21. / obr. 7. 68. (čtverec v základní rovině)
    • Přehled základních konstrukcí
  • krychle (CD př. 7. 18. / obr. 7. 56.)
  • jehlan (PDF)
  • schody (CD př. 7. 17. / obr. 7. 55.)
Asi není nastaveno vykreslování obrázků!
Asi není nastaveno vykreslování obrázků!
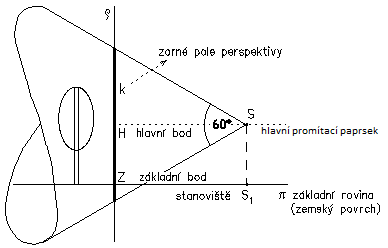
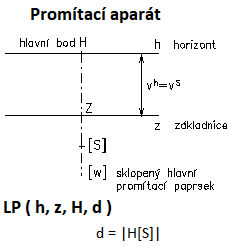
  9. Lineární perspektiva
  • Kružnice
    • v základní rovině (CD př. 7. 23. / obr. 7. 70.) PDF (chybná hlavička příkladu)
    • ve svislé rovině (CD př. 7. 24. / obr. 7. 71.) PDF
  • Válec s jednou podstavou v základní rovině
  • Průsečná metoda (jen k zadání rysu — Soubor CD-ROMů Deskriptivní geometrie / pro I. ročník Stavební fakulty VUT v Brně / Kap. 7. 4. Metody konstrukcí perspektivy – Průsečná metoda).
  • Šestiboký hranol s otvorem
  • Jehlan s podstavou kolmou k základní rovině
  • Brána s půlobloukem

10.
Rovnoběžné osvětlení
11. Rotační tělesa   
Řez rotačního protáhlého elipsoidu rovinou ρ v MP — osa kolmá na půdorysnu π, S[0;45;45], hlavní meridián a=40, b=30; ρ(–80;75;65).
12. Šroubovice:  vymodelování, vlastnosti, rozvinutí do roviny (Kochaňského rektifikace kružnice – Sobotkova), shrnutí, příklady využití.
  • Mongeova projekce — bod M, osa kolmá k půdorysně, výška závitu (půdorysem je kružnice, nárysem sinusoida); bodová konstrukce nárysu jako pohybující se bod M'2
    • Šroubovice, jako nejkratší spojnice dvou bodů na válcové ploše (Soubor CD-ROMů Deskriptivní geometrie / Další sbírky a výukové programy deskriptivní geometrie / Sbírka zkouškových příkladů z deskriptivní geometrie / 3. Šroubovice a šroubové plochy Příklad 4:)
  • Kolmá axonometrie — pravotočivá šroubovice, CD: … sbírka zkoušk. … 3. Příklad 6:
13. Konoidy     (Soubor CD-ROMů Deskriptivní geometrie / Deskriptivní geometrie pro kombinované studium pro I. ročník Stavební fakulty / 12. Zborcené plochy / 12. 3. Zborcené plochy vyšších stupňů / 12. 3. 1. Konoidy) ve stavebnictví

Další příklady na procvičení   NEBODOVANÉ!

Informace k zápočtu v zimním semestru 2022/2023

  1. KAŽDÁ neúčast na cvičení musí být OMLUVENA nebo NAHRAZENA!
  2. Odevzdané dva (zadání) RYSY – 5; 10 bodů
    (nejlépe na kladívkový papír) tužkou, popis šablonou (další pokyny pro zpracování rysů).
  3. Odevzdané tři (zadání) POVINNÉ úkoly – 3; 3; 4 body.
  4. Za odevzdání prací pouze v elektronické podobě je zisk pouze poloviny bodů.
  5. Ze cvičení student musí získat alespoň 10 bodů (z 35 možných).
    Získané body budou tvořit součást hodnocení u zkoušky (ze 100 možných bodů).

Informace ke zkoušce v zimním semestru 2022/2023

Ke studiu (mimo jiné) doporučuji:    1.   CD-ROM   Zde má být obrázek studijního CD-ROMu! Asi není nastaveno vykreslování obrázků.

2.   Autorský kolektiv Ústavu matematiky a deskriptivní geometrie FAST VUT v Brně: Sbírka řešených příkladů z KONSTRUKTIVNÍ geometrie, Stavební fakulta VUT v Brně, 2021. Souhrn řešených krokovaných příkladu z konstruktivní geometrie vytvořených převážně pomocí softwaru Zde má být logo GeoGebry! Asi není nastaveno vykreslování obrázků. , ale jsou zde vloženy i řešené krokované příklady ve formátu PDF vytvořené pomocí AutoCADu:


3.   případně      Zde mají být Elektronická skripta Fakulty architektury ČVUT! Asi není nastaveno vykreslování obrázků.      nebo      Konstruktivní geometrie FS VŠB-TUO

Zpět