8 Simulace nelineárního dynamického systému - pokračování
deterministický chaos
řídící parametry systému
zdvojování periody limitního cyklu
střídavý a metastabilní chaos
chaotický atraktor
Přidání další dimenze do našeho modelu rotátoru vytváří možnost jiného chování, které se v systémech omezených na plochu nevyskytuje. Ukazuje se se že alespoň tři nezávislé stavové proměnné jsou nutnou podmínkou pro existenci jevu, který se nazývá deterministický chaos (druhou nutnou podmínkou je přítomnost dostatečně silné nelineární složky v definici systému).
8.4 Trojrozměrný fázový prostor
Pokud bude na rotátor působit harmonická vynucující síla, bude její fáze q tvořit další stavovou proměnnou a fázový prostor již nebude rovinný. Pohybová rovnice systému bude:
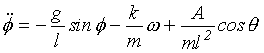 |
(8.5) |
kde A je amplituda působící síly a q = W.t je její fáze. Parametr W je úhlová frekvence síly. Odpovídající soustava dynamického systému je:
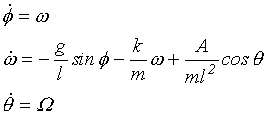 |
(8.6) |
Pro snížení počtu parametrů přepíšeme soustavu (8.6) do bezrozměrného tvaru, který poprvé použili Gwinn a Westervelt:
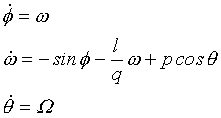 |
(8.7) |
q je tlumící koeficient a p koeficient amplitudy vnější síly.
Objekt rotátoru v našem příkladě musíme rozšířit o další stavovou proměnnou theta a parametry omg a p, které kvantifikují vnější sílu. Metodu step() pro výpočet nového stavu musíme rovněž patřičně modifikovat.
Pro zobrazení fázového portrétu použijeme stejnou metodu jako v předcházejících případech. Ignorováním proměnné q provádíme ve skutečnosti projekci prostorového fázového portrétu do roviny (f,w).
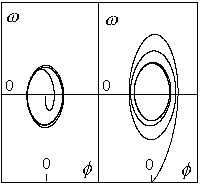
Obr.8.6a. Trajektorie pro parametry W=2/3, q=2, p=0.5
(slabá síla). Obrázky se liší počátečními podmínkami (f0,w 0). V obou případech systém dosáhne stejného
limitního cyklu.
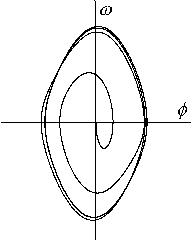
Obr.8.6b. Trajektorie ve stejném měřítku s větší koeficientem vnější
síly p=0.9. Systém se opět ustálil v limitním cyklu, tentokrát s větší amplitudou
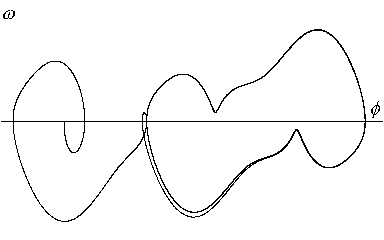
Obr.8.7. Parametr p=1.08. Systém se ustálil v limitním cyklu s poměrně
složitým průběhem.
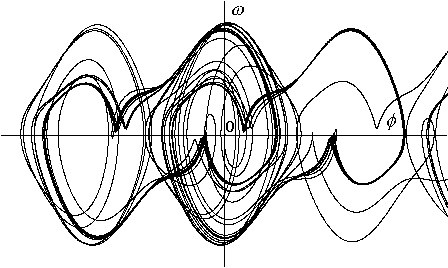
Obr.8.8 Trajektorie systému pro p=1.15 Systém se vyvíjí chaoticky. Pokud
dosáhne stavu připomínajícího limitní cyklus (viz obr.8.7), opět jej po určité
době opustí.
Z výše uvedených obrázků lze učinit několik závěrů:
8.5 Limitní množiny
Abychom zcela zmapovali dynamický systém tlumeného rotátoru buzeného harmonickou silou, museli bychom prověřit fázové portréty systému pro všechny hodnoty parametrů systému (p, q, W ), které se nazývají také řídící parametry. To je samozřejmě nemožné, neboť nelze rozumně popsat fázový portrét ani pro vhodně vybranou trojici řídících parametrů, kde se systém chová chaoticky. Pokusíme se proto přijmout některá omezení:
Na sérii obrázků 8.9a-m jsou trajektorie systému v ustáleném stavu pro poměrně úzkou škálu parametrů p. Vidíme, že vývoj systému se již pro malé změny parametru dramaticky mění od jednoduchého limitného cyklu až po chaotické chování a zpět k pravidelným cyklům. Charakteristické je tzv. zdvojování periody limitního cyklu skokem při malé změně řídícího parametru (viz obr.8.9b). Původně jednoduchá uzavřená křivka limitního cyklu se změní na dvojitou (bifurkace).
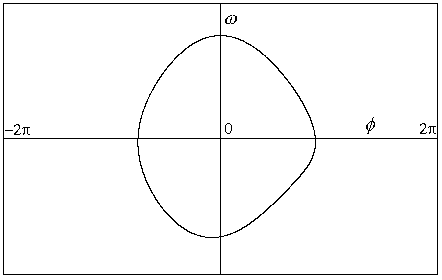
Obr.8.9a p=1.06
Jednoduchý limitní cyklus při projekci trajektorie do roviny (f,w).
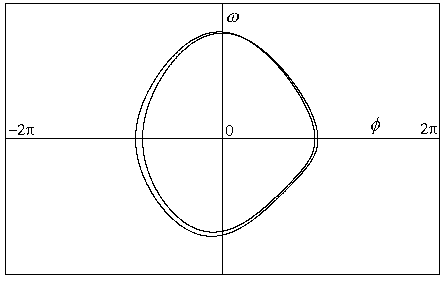
Obr.8.9b p=1.07
Zdvojení periody při malé změně řídícího parametru. Křížení
trajektorie je pouze zdánlivé, neboť je ve skutečnosti prostorová.
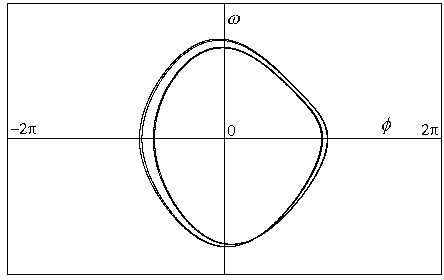
Obr.8.9c p=1.08
Další zdvojení periody. Původní cyklus je nyní čtyřnásobný.
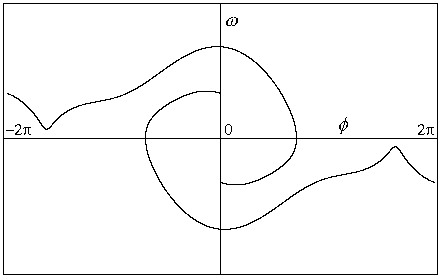
Obr.8.9d p=1.08
Jiný limitní cyklus pro stejný řídící parametr avšak trajektorie má jiné počáteční podmínky.
(U předcházejících hodnot řídícího parametru se tento typ limitního cyklu
nevyskytoval).
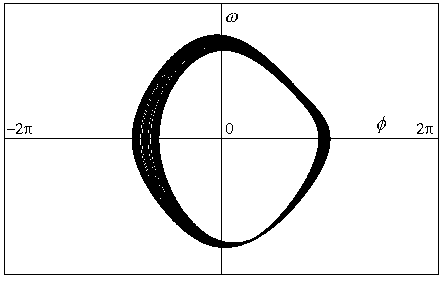
Obr.8.9e p=1.09
Pohyb systému je kvaziperiodický (viz odst.3.5.3). Trajektorie v ustáleném
tvaru vyplní "hustě" uzavřenou oblast projekce fázového prostoru, tj.
prochází v libovolné blízkosti každého bodu z této oblasti.
Obr.8.9f p=1.09
Jiný typ limitního cylu při stejném parametru. Trajektorie se liší
počátečními podmínkami.
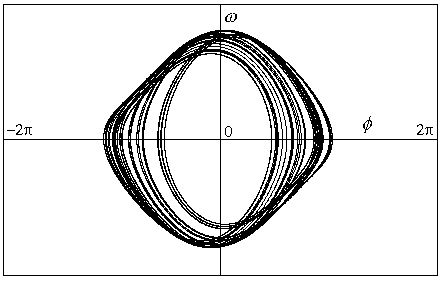
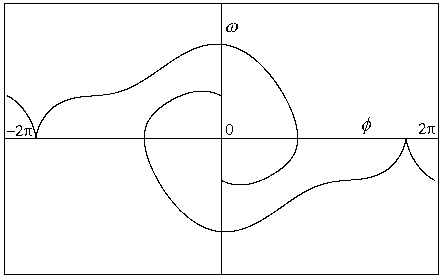
Obr.8.9g p=1.10
Limitní cyklus není kvaziperiodický, ale původní perioda je mnohokrát
zdvojena.
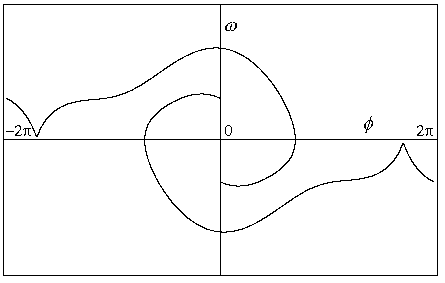
Obr.8.9h p=1.10
Druhý typ limitního cyklu pro jiné počáteční podmínky. Je zajímavé
sledovat spojité morfologické proměny tohoto cyklu při změně řídícího parametru.
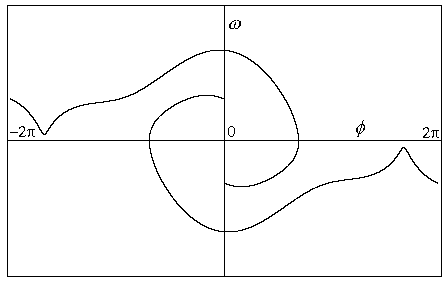
Obr.8.9i p=1.11
Původní typ cyklu zanikl, druhý typ limitného cyklu se dále proměňuje. Dva
body, ve kterých prakticky neexistuje derivace, odpovídají poklesu rychlosti rotátoru
k nule a opětné obnovení pohybu stejným směrem.
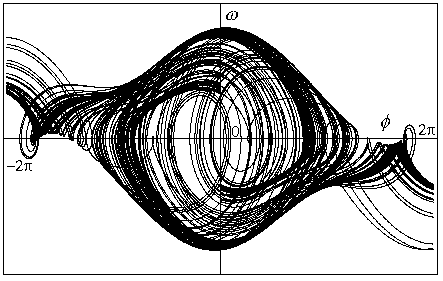
Obr.8.9j p=1.15
Chaotická trajektorie. Pohyb systému zůstavá omezen na podmnožinu fázového
prostoru (limitní množinu), která není kompaktní. Taková limitní množina se
nazývá podivný atraktor (viz dále).
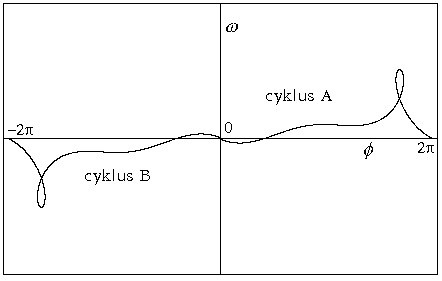
Obr.8.9k p=1.30
Systém v ustáleném stavu opět dospěje k limitnímu cyklu. Na obr. jsou ve
skutečnosti dva symetrické typy cyklů v levé a pravé části obrázku. Cykly se
liší počátečními podmínkami trajektorie.
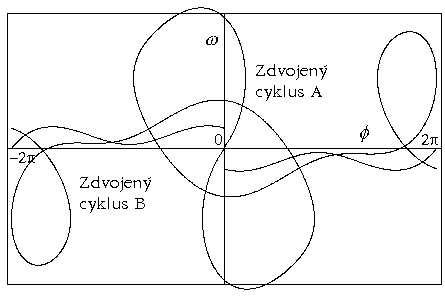
Obr.8.9l p=1.45
Další vývoj dvou limitních cyklů z předcházejícího obrázku. Došlo
rovněž ke zdvojení periody.

Obr.8.9m p=1.50
Jiný typ chaotické trajektorie. Je zajímavé srovnat oba typy chaosu, které
nastávají pro poměrně blízké hodnoty řídícího parametru. V obou případech lze
rozeznat oba typy stabilních limitních cyklů.
Na obr.8.10 je průběh kinetické energie rotátoru pro hodnoty řídícího parametru, které zaručují limitní cyklus prvního a druhého typu a chaotický vývoj (viz obr.8.9a,h,j). Průběh energie (získaný metodou showE()) dobře dokumentuje představu vyplývající z průběhů trajektorií o chaotickém chování jako o náhodných přechodech mezi více typy limitních cyklů. Přechody systému na chaotické chování jsou klasifikovatelné podle několika mechanizmů. Teorie bifurkací rozeznává několik typů chaosu (střídavý chaos, metastabilní chaos atd.), které jsou závislé na stavech systému před vznikem chaosu. V našem případě je rozhodující při rostoucím parametru p existence několika typů stabilních limitních cyklů, jejichž interakcí vznikne chaotický atraktor.
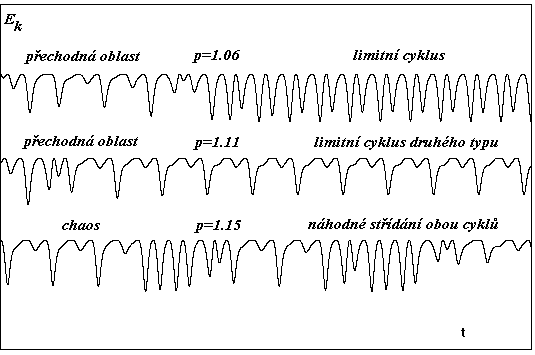
Obr.8.10 Průběh kinetické energie pro různé hodnoty řídícího
parametru. Patrné je ustalování systému do limitních cyklů a přítomnost obou typů
cyklů v chaotickém průběhu.