5 Konzervativní systémy
zobecněné souřadnice a hybnosti
Hamiltonovy rovnice
Liouvilleův teorém
cyklické souřadnice
kanonické transformace a normalizovaný tvar
integrabilní konzervativní systémy
homoklinické a heteroklinické body5.1 Liouvilleův teorém a cyklické souřadnice
5.2 Integrabilní systémy a pohyb na invariantním toru
5.3 Neintegrabilní systémy
Konzervativní dynamický systém má alespoň jeden integrál pohybu, kterým je obvykle
Hamiltonova funkce ![]() , závislá na zobecněných souřadnicích
qi a hybnostech pi systému, což jsou zřejmě také
proměnné dynamického systému. Připomínáme, že v Hamiltonově pojetí jsou
souřadnice i hybnosti zcela rovnocenné a pro systém s n stupni volnosti má tedy
fázový prostor dimenzi 2n. Hamiltonovy kanonické rovnice, které lze chápat také
jako definiční rovnice dynamického systému, jsou
, závislá na zobecněných souřadnicích
qi a hybnostech pi systému, což jsou zřejmě také
proměnné dynamického systému. Připomínáme, že v Hamiltonově pojetí jsou
souřadnice i hybnosti zcela rovnocenné a pro systém s n stupni volnosti má tedy
fázový prostor dimenzi 2n. Hamiltonovy kanonické rovnice, které lze chápat také
jako definiční rovnice dynamického systému, jsou
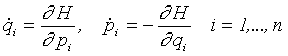 |
(5.1) |
Každá trajektorie systému v takto definovaném systému je však omezena na podmnožinu fázového prostoru zákonem zachování energie
| (5.2) |
Vztah (5.2) představuje omezující podmínku, která připouští pohyb pouze na povrchu (2n-1)-rozměrné variety umístěné ve fázovém prostoru.
5.1 Liouvilleův teorém a cyklické souřadnice
Podle Liouvilleova teorému
se zachovává u konzervativních systémů podél trajektorií tzv. fázový objem, což
můžeme přeformulovat následujícím způsobem: nechť souvislá podmnožina G fázového prostoru má objem m(G).
Stanovme počáteční podmínky tak, aby každým bodem množiny G
procházela právě jedna trajektorie konzervativního systému v čase t=0.
Operátor toku Ft aplikovaný na množinu G ji pak zobrazí do množiny ![]() , která obsahuje body stejných trajektorií v čase t. Podle
Liovilleova teorému je
, která obsahuje body stejných trajektorií v čase t. Podle
Liovilleova teorému je![]() pro každé t.
Teorém tedy vylučuje přítomnost atrakčních množin a atraktorů ve fázových portrétech
konzervativnách systémů. Vzhledem k zachování fázového objemu by totiž tok na
atraktoru musel nabývat nekonečných hodnot (např. v případě limitního cyklu
rovinného systému má cyklus proti oblasti přitažlivosti nulový objem a Liovilleův
teorém nemůže platit). Přítomnost atraktorů je tedy charakteristická pro
nekonzervativní (např. disipativní) systémy.
pro každé t.
Teorém tedy vylučuje přítomnost atrakčních množin a atraktorů ve fázových portrétech
konzervativnách systémů. Vzhledem k zachování fázového objemu by totiž tok na
atraktoru musel nabývat nekonečných hodnot (např. v případě limitního cyklu
rovinného systému má cyklus proti oblasti přitažlivosti nulový objem a Liovilleův
teorém nemůže platit). Přítomnost atraktorů je tedy charakteristická pro
nekonzervativní (např. disipativní) systémy.
Pokud má systém více integrálů pohybu (např. hybnost, moment hybnosti apod.), je
pohyb systému redukován na povrch variety ještě nižší dimenze: pro k
integrálů pohybu, (které můžeme chápat jako k omezujících podmínek), je
dimenze variety zřejmě 2n-k. Uvažujme speciální případ, kdy existuje právě
n integrálů pohybu a zároveň Hamiltonián ![]() nezávisí explicitně na žádné zobecněné souřadnici qi
, tj. podle (5.1) je
nezávisí explicitně na žádné zobecněné souřadnici qi
, tj. podle (5.1) je
| (5.3) |
Všechny zobecněné hybnosti jsou tedy integrálem pohybu. Pak ovšem podle (5.1) platí
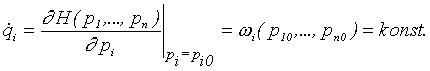 |
(5.4) |
odkud
| (5.5) |
Souřadnice qi, na nichž Hamiltonián explicitně nezávisí se nazývají cyklické, neboť podle jejich závislosti na čase vyjádřené vztahem (5.5) mají obvykle význam úhlu, tj.
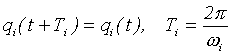 , kde Ti je perioda
cyklické souřadnice.
, kde Ti je perioda
cyklické souřadnice.
Poznámka:
Periodický charakter cyklických souřadnic v případě nechaotického pohybu je vynucen
omezením pohybu systému na podmnožinu fázového prostoru.
5.2 Integrabilní systémy a pohyb na invariantním toru
Konzervativní systém samozřejmě může mít tolik integrálů pohybu, kolik má stupňů volnosti, a přesto je jeho Hamiltonián explicitně závislý na některých (nebo všech) zobecněných souřadnicích a vztahy (5.3-5) pak neplatí. Pomocí kanonických transformací proměnných však lze systém transformovat do tvaru, kdy Hamiltonián nezávisí na souřadnicích (tzv. normalizovaný tvar, i když nalezení patřičné transformace může být stejně náročné, jako samotné řešení systému. Připomínáme, že kanonické transformace při přechodu k jiným stavovým proměnným ponechávají tvar Hamiltonových rovnic (5.1) invariantní. Blíže se teoretickou mechanikou nebudeme zabývat, uvedená tvrzení jsou dostupná v běžných učebnicích.
Konzervativní systémy, které lze transformovat do normalizovaného tvaru se nazývají integrabilní (lze ukázat, že systémy s jedním stupněm volnosti a anlyticky vyjádřitelným Hamiltoniánem jsou vždy integrabilní). Z hlediska klasifikace dynamických systémů vidíme podle vztahů (5.3) a (5.4), že se jedná o lineární systémy (jsou tedy řešitelné) a normalizovaná matice jejich pohybu má obecně tvar
rozložitelný na submatice
,
tj. jejich pohyb lze podle odst.3.8 znázornit jako n nezávislých kruhových pohybů (pro každý stupeň volnosti jeden). Pro n=2 se jedná topologicky o pohyb na dvourozměrném toru, pro větší n leží trajektorie systému na n-rozměrném toru. Tento torus se nazývá také invariantním, neboť odpovídá definici invariantní množiny podle definice z odst.4.2. Často se hovoří o invariantním toru i v souvislosti s plochou kolmého řezu torem v Poincarého mapách (viz dále). Dá se totiž ukázat, že pro nechaotické pohyby je plocha vzhledem k místě řezu konstantní (samotný torus může být však komplikovaně deformován).
Poznámka:
Fakt, že pohyb integrabilního systému leží na povrchu toru je z topologického
hlediska zřejmý. Torus je jediným topologickým útvarem, který vyhovuje podmínce
absence limitních množin. Např. povrch koule této podmínce vyhovovat nemůže, což
si lze názorně představit jako úlohu “učesat chlupatou kouli bez pěšinek a
vírů”. Je zřejmé, že na povrchu koule je úloha neřešitelná, avšak na povrchu
toru je snadná.
Poincarého mapa integrabilního systému, zkonstruovaná jako řez rovinou obsahující osu toru, je pak zřejmě tvořena soustavou bodů ležících na uzavřené křivce. Pokud jsou hodnoty frekvencí jednotlivých pohybů wi vzájemně racionálně závislé, bude počet těchto bodů konečný (periodický pohyb), v opačném případě body vyplní celou křivku (kvaziperiodický pohyb). Fázový portrét obecně neintegrabilního systému mohou v případě slabých nelinearit opět tvořit trajektorie na povrchu toru, avšak i pro jednu hodnotu energie může být přípustných torů mnoho podle počátečních hodnot stavových proměnných, které vyhovují podmínce konstantní energie.
Obr.5.1 Soustava dvourozměrných torů popisjících pohyb konzervativního systému se dvěma stupni volnosti. Různá tloušťka torů je dána např. různým zastoupením průměrné kinetické a potenciální energie v celkové energii systému.
5.3 Neintegrabilní systémy
Některé aspekty neintegrabilních konzervativních systémů budeme ilustrovat na konkrétním systému kvůli obtížnosti obecné analýzy. Použijeme známý model, který kvalitativně objasňuje průběh vibračního spektra molekul vody. Model zavádí dva stupně volnosti, každý odpovídá jedné vazbě atomů H-O. Je zřejmé, že pro přílišnou délku vazby q dojde k jejímu přerušení, což kvalitativně popisuje tzv. Morseův potenciál
| (5.6) |
kde koeficient D odpovídá vazebné disociační energii.
Hamiltonián systému lze psát ve tvaru
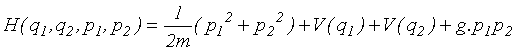 |
(5.7) |
kde první člen odpovídá kinetické energii, druhý a třetí člen vyjadřuje potenciální vazební energii s průběhem podle (5.6) a poslední (nelineární) člen kvalitativně postihuje vzájemné ovlivňování obou vazeb (např. prostřednictvím rozkmitání těžkého atomu kyslíku). Při malé energii molekuly jsou výchylky atomů od rovnovážné polohy malé a Morseův petenciál lze aproximovat kvadratickou závislostí. Systém je pak integrabilní a normalizovaný tvar lze dostat po transformaci do nových souřadnic:
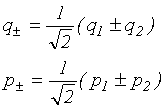 |
(5.8) |
Vlastní frekvence molekuly jsou pak
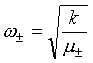 |
(5.9) |
kde koeficient ![]() a
a 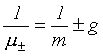 .
.
Část trajektorie systému promítnuté do roviny ![]() (dráha v normalizovaných souřadnicích) je uvedena na obr.5.2(a).
Tvoří ji de facto známé Lissajousovy obrazce, neboť průběh normalizovaných
souřadnic je harmonický. Kružnice vyjadřuje hranice, kdy veškerá energie systému je
pouze potenciální. Je zřejmé, že některé body vratu promítnuté trajektorie
odpovídající nulové rychlosti musí ležet na této kružnici. Rovné hranice obálky
trajektorie jsou důsledkem integrability systému. Odpovídající Poincarého mapa na
obr. 5.2(b) je zkonstruována pomocí podmínek
(dráha v normalizovaných souřadnicích) je uvedena na obr.5.2(a).
Tvoří ji de facto známé Lissajousovy obrazce, neboť průběh normalizovaných
souřadnic je harmonický. Kružnice vyjadřuje hranice, kdy veškerá energie systému je
pouze potenciální. Je zřejmé, že některé body vratu promítnuté trajektorie
odpovídající nulové rychlosti musí ležet na této kružnici. Rovné hranice obálky
trajektorie jsou důsledkem integrability systému. Odpovídající Poincarého mapa na
obr. 5.2(b) je zkonstruována pomocí podmínek ![]() .
Druhá z podmínek vylučuje z kolmého řezu toru druhou (protilehlou) část. Plná
vnější kružnice opět vyjadřuje hranice dané celkovou energií systému.
.
Druhá z podmínek vylučuje z kolmého řezu toru druhou (protilehlou) část. Plná
vnější kružnice opět vyjadřuje hranice dané celkovou energií systému.
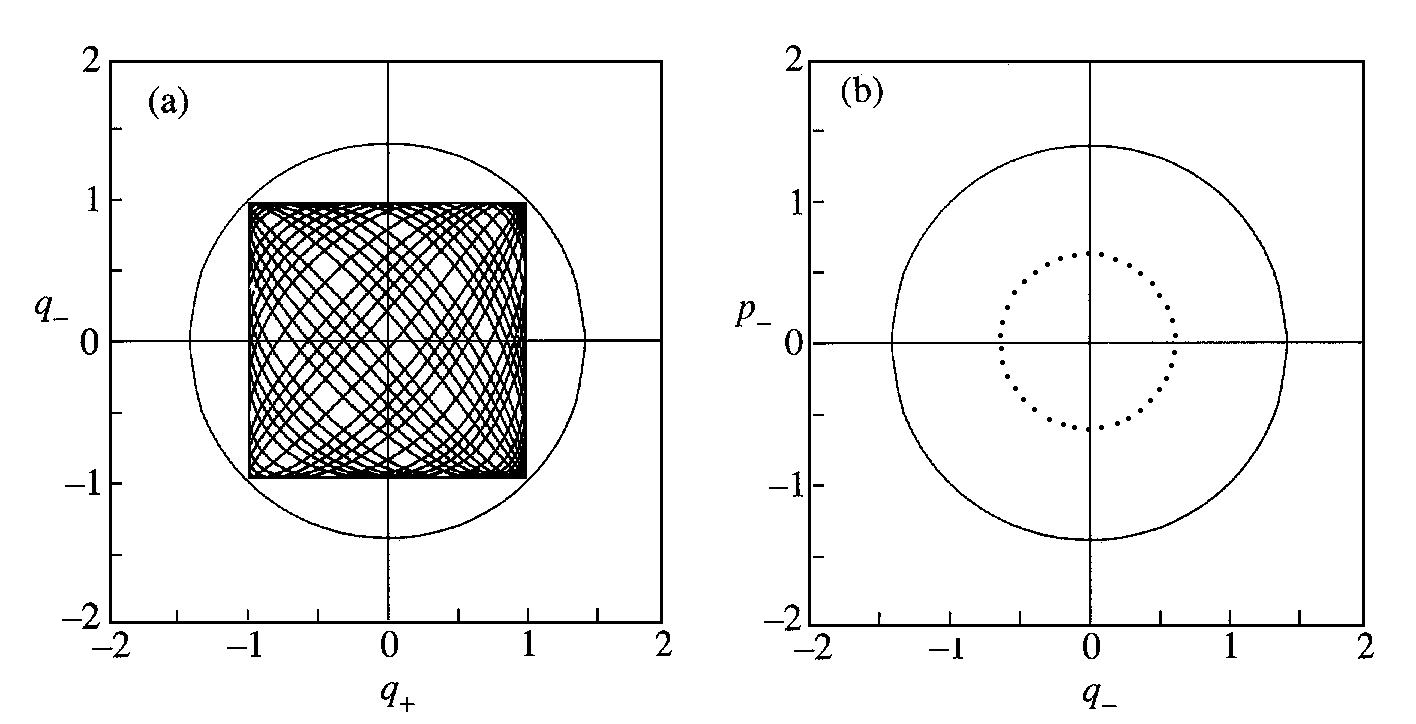
Obr.5.2 Část trajektorie systému (5.7) v normalizovaném tvaru aproximovaného kvadratickým potenciálem a odpovídající mapa Poincarého.
Poznámka:
Jednotky v dále uváděných diagramech jsou pro souřadnice ![]() a pro hybnosti
a pro hybnosti ![]() , kde
, kde ![]() . Z toho ihned plyne, že energie je uváděna v
přirozených jednotkách
. Z toho ihned plyne, že energie je uváděna v
přirozených jednotkách ![]() a že systém je
normován do bezrozměrného tvaru vztahem
a že systém je
normován do bezrozměrného tvaru vztahem ![]() .
.
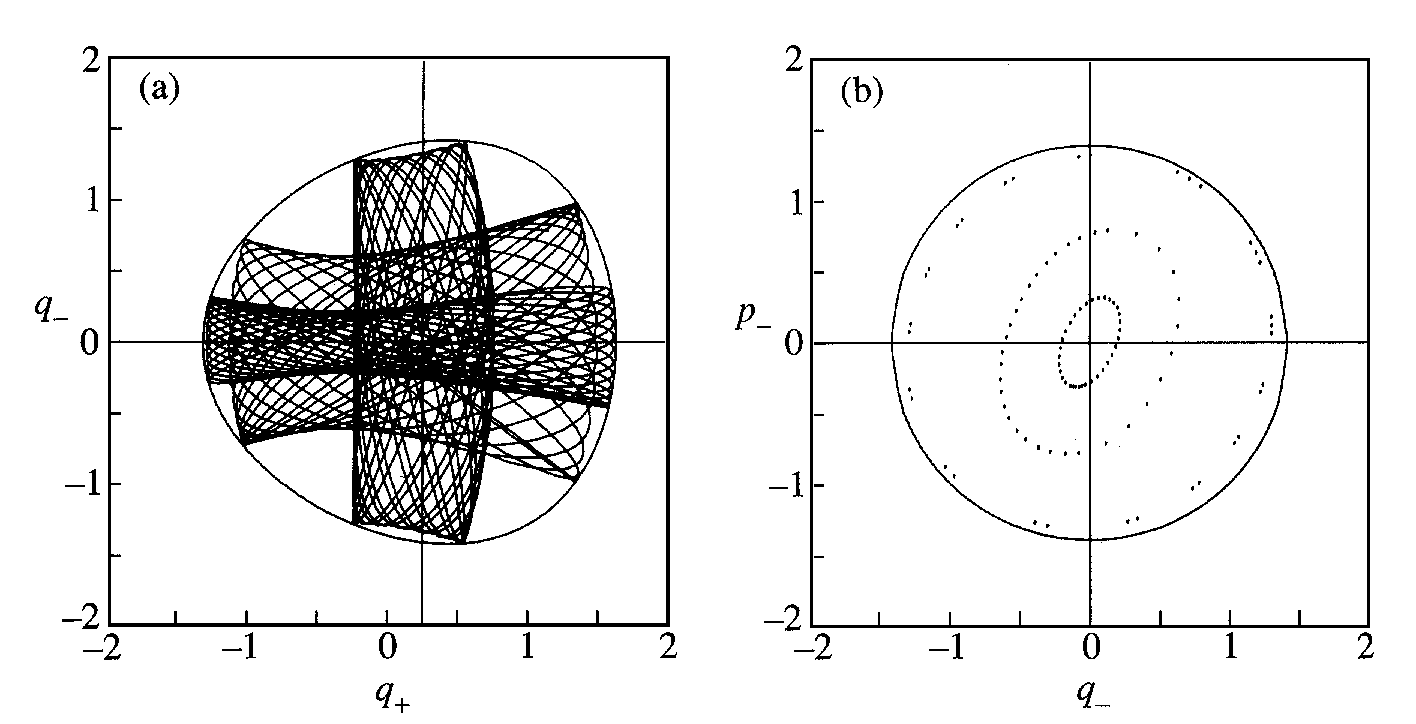
Obr.5.3 Úsek promítnuté trajektorie (a) při vyšší celkové energii systému pro různé počáteční podmínky. Hranice obálek je již zřetelně zakřivena, což indikuje neintegrabilitu systému. Odpovídající Poincarého mapy jednotlivých trajektorií (b) tvoří soustavu soustředných elips. Větší energie tedy nezměnila kvalitativní chování systému proti jeho lineární formě.
Na obr. 5.4 jsou trajektorie systému při ještě vyšší celkové energii. Dvě kvalitativně odlišné trajektorie signalizují, že v chování systému došlo k podstatným změnám. Při této energii je možný takový pohyb systému, kdy většina energie je trvale lokalizována na jednu z vazeb systému (tzv. lokální mód), avšak je možný i normální pohyb systému, kdy je průměrná energie obou vazeb stejná. Odpovídající Poincarého mapy těchto druhů pohybů jsou kvalitativně odlišné. V normálním módu je Poincarého mapa tvořena deformovaným oválem, zatímco v lokálních módech se jedná přibližně o elipsy s excentrickými středy. Dva lokální módy jsou symetrické podle středu.
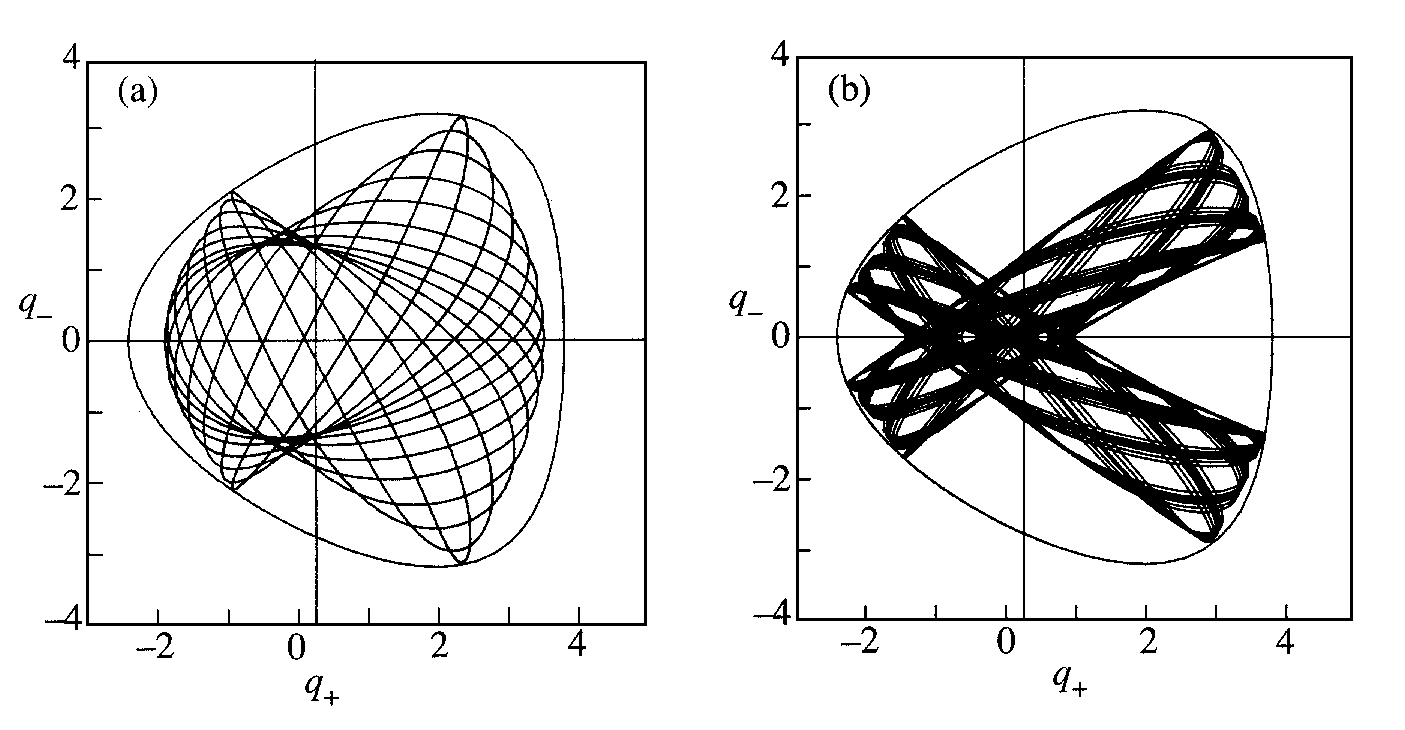
Obr. 5.4 Normální (a) a dvě symetrické lokální trajektorie (b) a odpovídající mapy Poicarého (c). Energie systému (E=4) je dostatečná k uplatnění neharmonického průběhu potenciálu. Mapa připomínající osmičku odpovídá kritické trajektorii oddělující dva kvalitativně odlišné druhy chování.
Z fyzikálního hlediska je normální mód charakterizován takovým průběhem
potenciálu, který umožňuje při vhodných amplitudách obou vazeb (počáteční
podmínky) vzájemné předávání energie frekvencí ![]() , zatímco v lokálním módu již neharmonický průběh potenciálu
při určitém poměru amplitud vazeb nedovolí přenos energie. Pro malé energie lze
závislost frekvencí na amplitudě zanedbat, a proto se vyskytují pouze normální
módy. Absorbční spektra molekul výskyt lokálních módů od určité excitační
energie potvrzují. Velikost energie systému je dost velká na to, aby bylo oprávněné
použití kvaziklasického přiblížení bez kvantových efektů. Vidíme, že i v
klasické mechanice se vyskytují jevy známé z kvantové mechaniky: přítomnost více
módů v důsledku změny symetrie systému jsou analogií kvantové degenerace stavů.
, zatímco v lokálním módu již neharmonický průběh potenciálu
při určitém poměru amplitud vazeb nedovolí přenos energie. Pro malé energie lze
závislost frekvencí na amplitudě zanedbat, a proto se vyskytují pouze normální
módy. Absorbční spektra molekul výskyt lokálních módů od určité excitační
energie potvrzují. Velikost energie systému je dost velká na to, aby bylo oprávněné
použití kvaziklasického přiblížení bez kvantových efektů. Vidíme, že i v
klasické mechanice se vyskytují jevy známé z kvantové mechaniky: přítomnost více
módů v důsledku změny symetrie systému jsou analogií kvantové degenerace stavů.
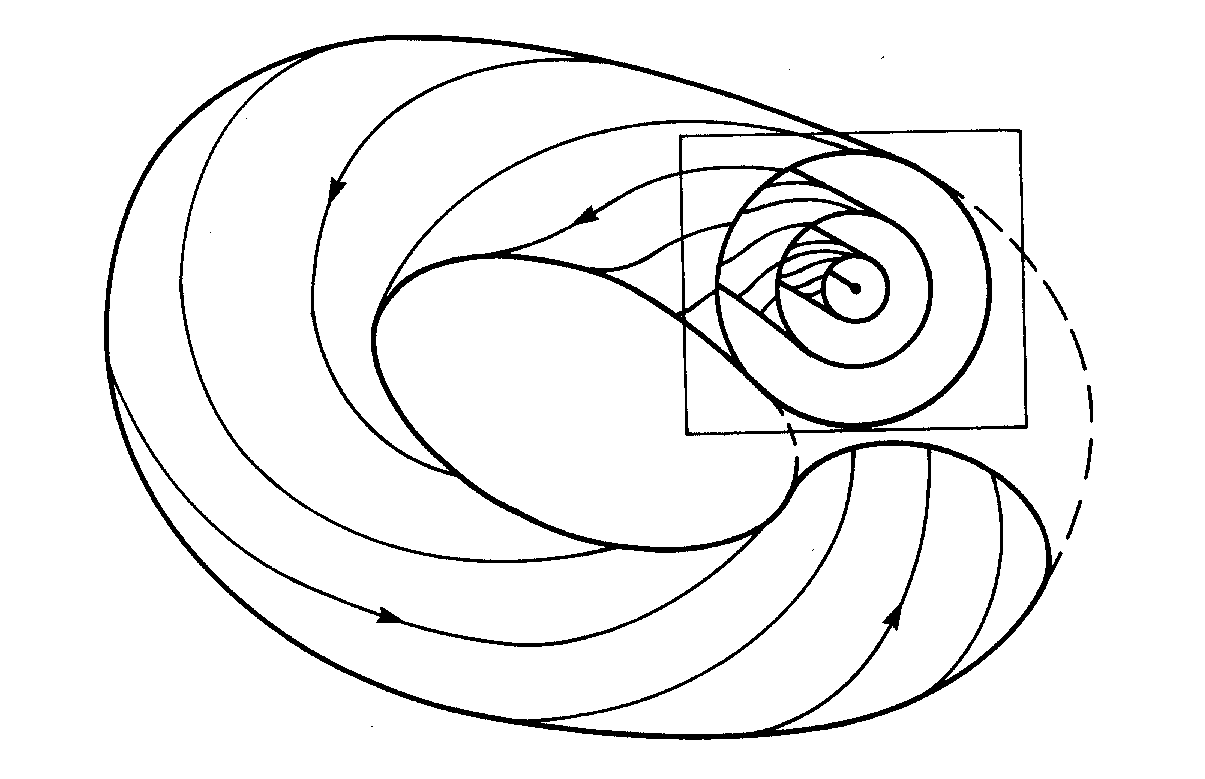
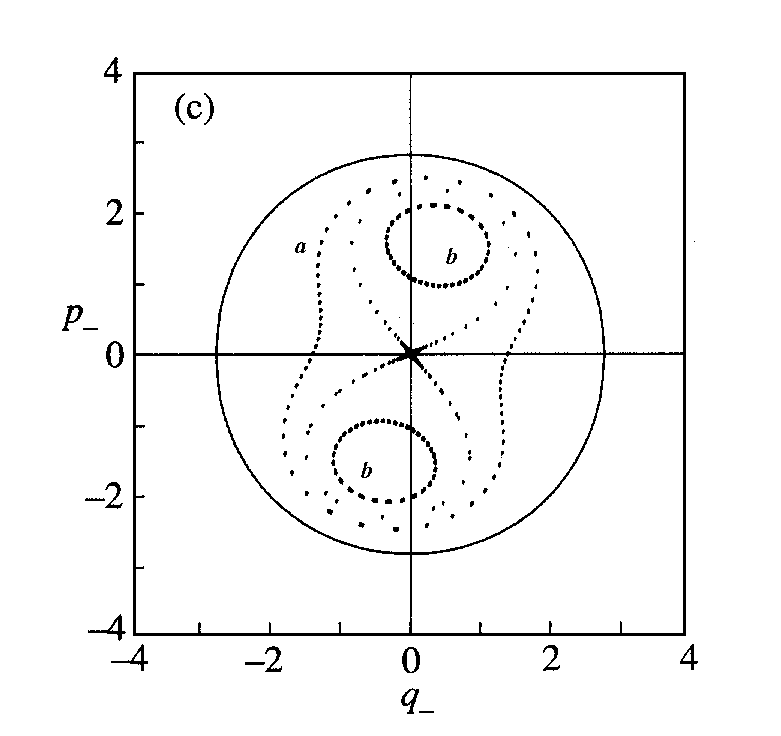
Poincarého mapu soustavy trajektorií lze parametrizovat celkovou energií systému. Pro malé hodnoty energií má Poincarého mapa v počátku stabilní pevný bod, od určité kritické hodnoty energie je však tento bod nestabilní (sedlový bod) a vznikají dva stabilní pevné body, které se od počátku s rostoucí energií systému vzdalují. Změna chování systému v okolí kritické energie se nazývá strukturální nestabilita systému a kvalitativní změna Poincarého mapy uvedeného typu je tzv. vidličková bifurkace (jeden pevný bod je nahrazen dvěma, které se od sebe rychle vzdalují při rostoucí hodnotě parametru - viz kap.6). Mapa obsahující počátek odděluje oblasti odlišného chování a tvoří tedy separatrix. Představuje řez speciální trajektorií takovou, že malá změna počátečních podmínek (samozřejmě vyhovující požadavku na stejnou celkovou energii systému) způsobí přechod na trajektorii s kvalitativně odlišným průběhem. Sedlový bod S uprostřed separatrix spojuje stabilní a nestabilní variety, které jsou tvořeny de facto jedinou varietou. K velmi důležitému jevu dojde při dalším zvyšování energie systému. Obě variety vycházející ze sedlového bodu již nesplývají, ale protínají se v tzv. homoklinickém bodě. Jeho vlastnosti jsou neobvyklé: další průchod trajektorie původně procházející homoklinickým bodem rovinou Poincarého mapy musí totiž opět ležet v obou varietách současně. Připomeňme, že jak stabilní, tak nestabilní varieta obsahují body, které se mapují do bodů téže variety a blíží, resp. vzdalují se od sedlového bodu. Znamená to, že homoklinický bod X se mapuje difeomorfismem P(X) do bodu, v němž opět leží průnik obou variet. Totéž ovšem platí i o bodu P2(X) atd. Protne-li se tedy stabilní a nestabilní varieta v homoklinickém bodě, musí se obě variety protínat opět v dalších bodech odpovídajících dalším průnikům trajektorie rovinou řezu (viz obr.5.5)
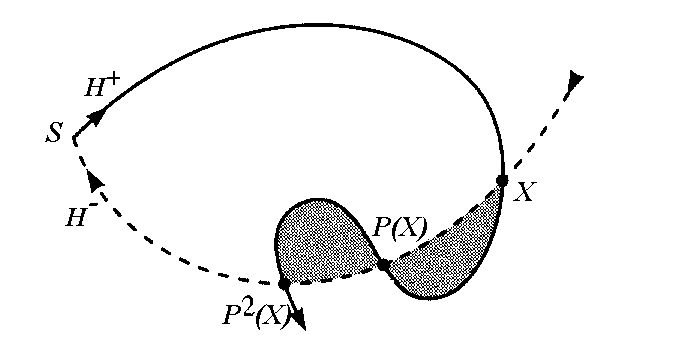
Obr. 5.5 Stabilní a nestabilní variety H+ a H- vycházející ze sedlového bodu S se protnou v homoklinickém bodě X. Další body P(X), P2(X) atd. musí opět ležet na obou varietách. Plocha uzavřená varietami je stejná.
Vzhledem k tomu, že k nestabilnímu sedlovému bodu se každá mapovaná posloupnost bodů obou variet limitně blíží, znamená to, že počet průniků obou variet roste nade všechny meze a směrem k sedlovému bodu se úměrně zvyšuje také jejich hustota. Navíc však lze ukázat, že plocha uzavřená oběmi varietami mezi dvěma následnými průniky je stejná (důsledek Liouvilleova teorému) a proto posloupnost následujících ploch mezi průniky musí tvořit stále užší a protáhlejší smyčky, jejichž délka v okolí sedlového bodu opět roste nade všechny meze. Schematicky je posloupnost deseti mapovaných bodů našeho systému zobrazena na obr.5.6. Vidíme, že původní dobře definované posloupnosti bodů z obr.5.4(c) jsou nyní neuspořádané.
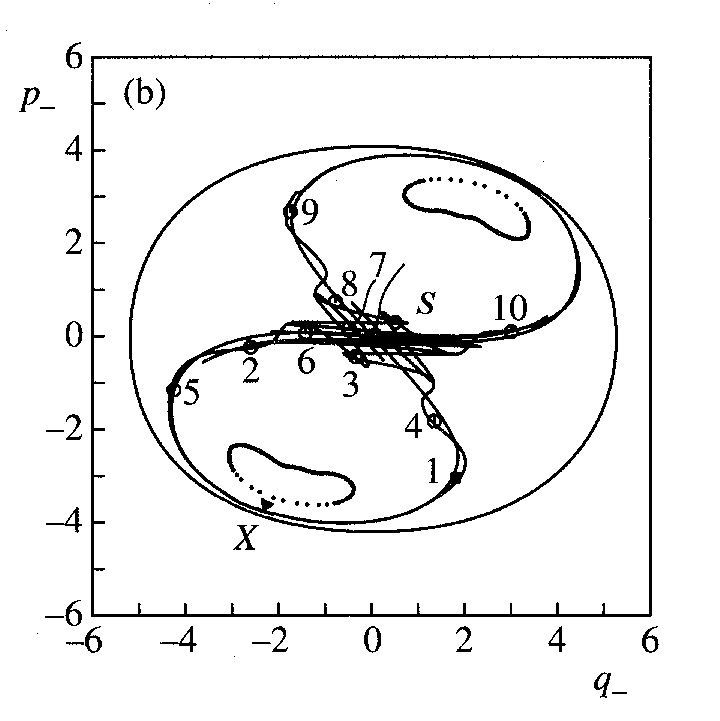
Obr. 5.6 Schematické zobrazení stabilní a nestabilní variety při vyšších energiích systému a posloupnost deseti po sobě následujících průchodů kritcké trajektorie rovinou Poincarého mapy. V homoklinickém bodě se obě variety protínají pod velmi malým úhlem, v okolí sedlového bodu jsou průniky prakticky pod stejným úhlem jako spojení původních neporušených variet bez homoklinického bodu. Vidíme rovněž, že vyznačené body posloupnosti na jedné z variet neleží na následujících smyčkách homoklinických průniků.
Na obr.5.7 je skutečná Poincarého mapa odpovídající popisovanému modelu homoklinických průniků. Lokální módy jsou i nadále dobře definovány, tj. existují trajektorie ležící na toru. Některé trajektorie již však na toru neleží, jejich Poincarého mapa je neuspořádaná a systém se pohybuje chaoticky. Počítačové modelování takové trajektorie je z hlediska zachycení dlouhodobějšího vývoje nemožné, což vyplývá z charakteru homoklinických průniků. V okolí sedlového bodu sebemenší zaokrouhlovací chyba může způsobit umístění nového mapovaného bodu ze stabilní na nestabilní varietu (tj. fatální chybu, která zcela mění charakter hledané posloupnosti).
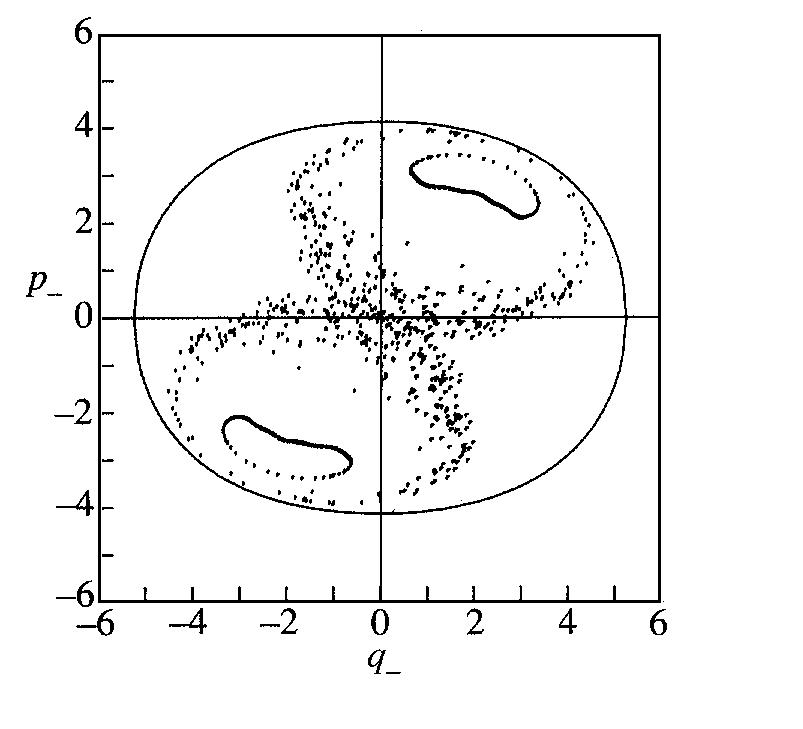
Obr.5.7 Poincarého mapa systému pro velikost energie E=8. Trajektorie v okolí separatrix má neuspořádanou Poincarého mapu, systém se chová chaoticky. Některé trajektorie v lokálních módech jsou nadále “rozumné” a predikovatelné.
Uvedený mechanizmus vzniku chaotického chování není doménou konzervativních systémů, jak dále uvidíme. U disipativních systémů je chaotické chování naopak průhlednější a lépe klasifikovatelné. Přesto je pro všechny druhy systémů přítomnost chaosu spjata s výskytem bifurkací různého druhu a s vzájemnou interakcí stabilních a nestabilních variet, které nemusí náležet jenom k jednomu nestabilnímu (sedlovému) bodu. V případě průniku variet náležejících různým kritickým bodům hovoříme o heteroklinickém průniku a heteroklinických bodech, neobvyklé vlastnosti tohoto jevu jsou však analogické homoklinickým průnikům.

Obr.5.8 Poincarého mapa nelineárního konzervativního systému s
mnohonásobnými invariantními tory oddělenými difuzními oblastmi chaotických
trajektorií. Oblast složitě proplétaných torů má fraktálový charakter.