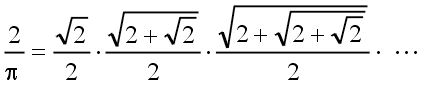
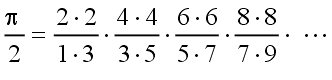
G. W. Leibniz (1646 – 1716)
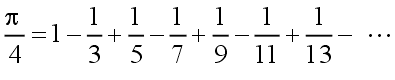
neboli
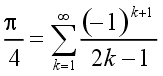
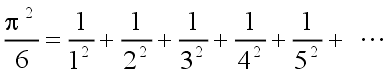
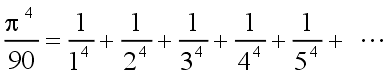
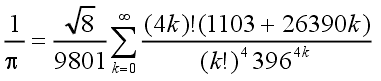
| F. Vieta (1540 – 1603) | 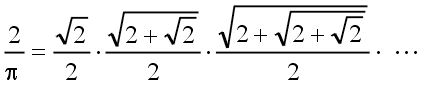 | (1) |
| F. Wallis (1616 – 1703) | 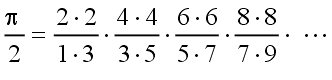 | (2) |
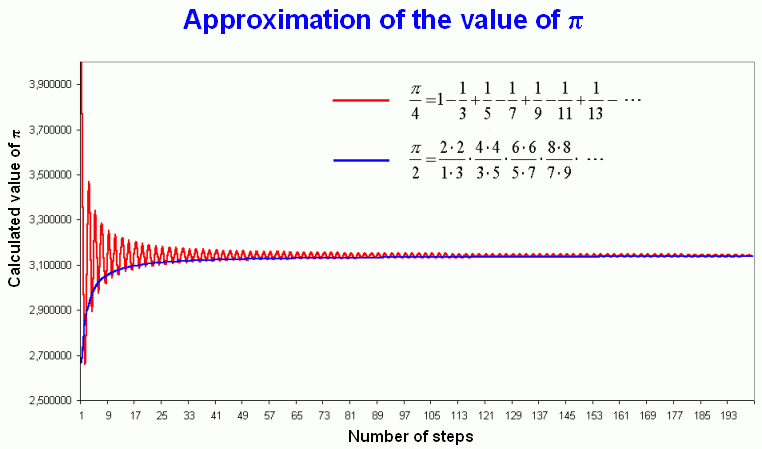
| J. Gregory (1638 – 1675), G. W. Leibniz (1646 – 1716) | 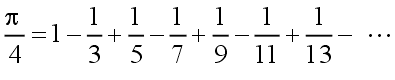 neboli 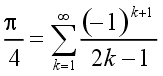 | (3) |
| L. Euler (1707 – 1783) | 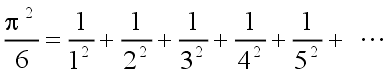 | (4) |
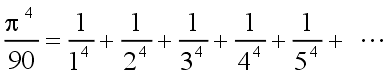 | (5) | |
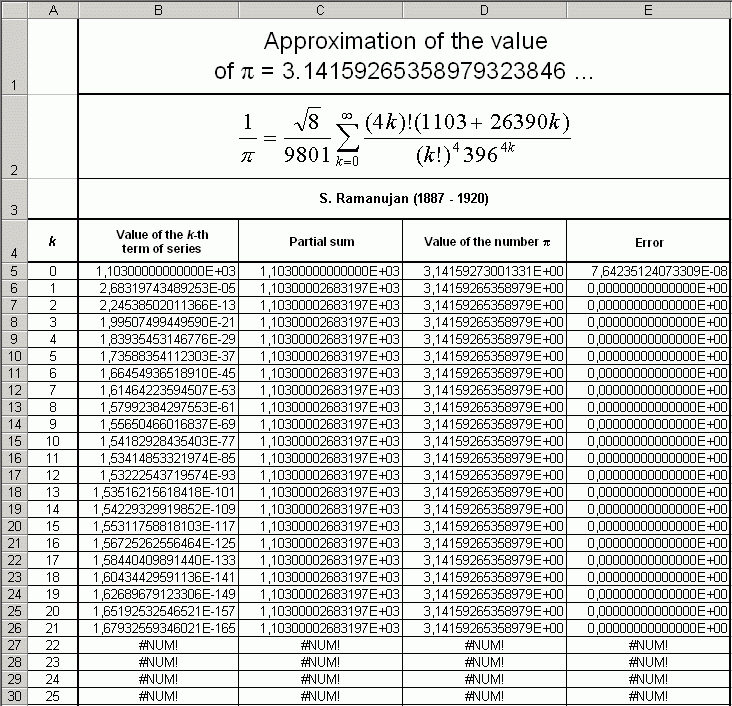
| S. Ramanujan (1887 – 1920) | 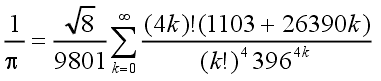 | (6) |
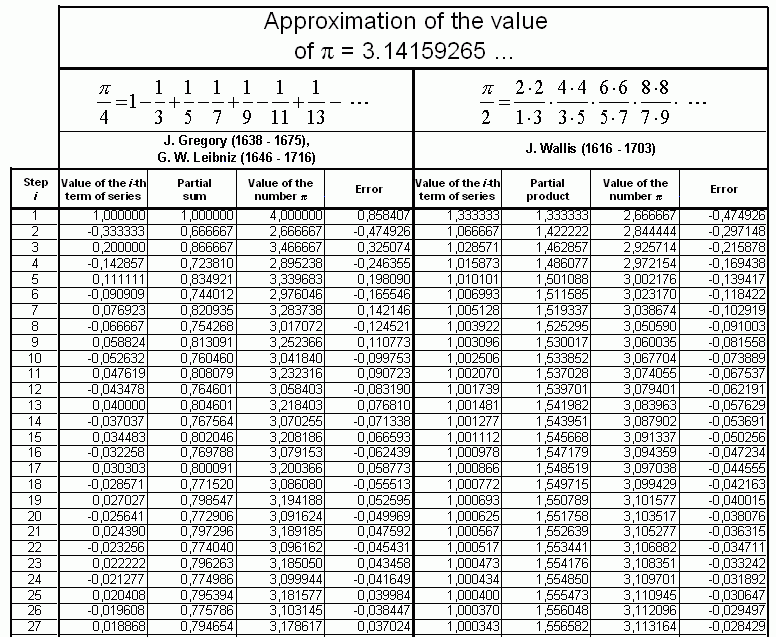
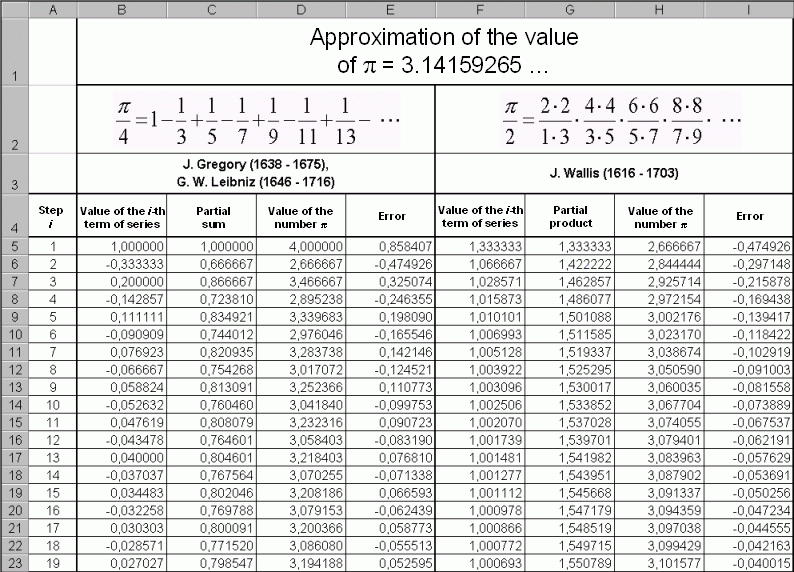
| SUM( ... ) | Adds all the numbers given as arguments and returns the sum. |
| PRODUCT( ... ) | Multiplies all the numbers given as arguments and returns the product. |
| PI() | Returns the mathematical constant π, accurate to 15 digits. |
| POWER(number;power) | Returns the result of a number raised to a power. |
| SQRT(number) | Returns a positive square root. |
| FACT(number) | Returns the factorial of a number. |