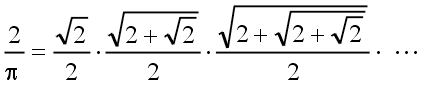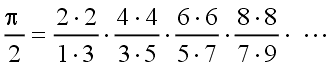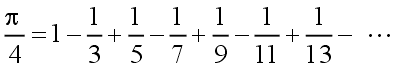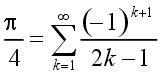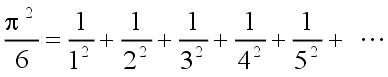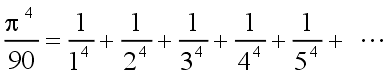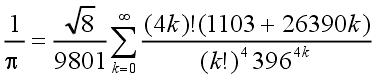Prémiové příklady

Vyřešené příklady lze odevzdat v písemné nebo elektronické formě kdykoliv do konce letního semestru 2003/2004. U každého vyřešeného příkladu vysvětlete funkci skriptu (význam použitých proměnných, popis použitého algoritmu apod.) a uveďte jeho úplný zdrojový kód. Není-li uvedeno jinak, vstup a výstup dat řešte užitím formuláře. Součástí hodnocení je též typografická a jazyková úroveň textu.

Sada 1

1. Francouzský expresní vlak TGV má stanovenou průměrnou rychlost 216 km/h. Nejvyšší přípustná velikost dostředivého zrychlení při průjezdu zatáčkou je pro pohodlí cestujících dána hodnotou 0.050g. Jaký je nejmenší možný poloměr zatáčky, kterou může vlak projíždět uvedenou rychlostí? Musí vlak v zatáčce o poloměru 1.00 km zpomalit? Na jakou rychlost?
   
   [JavaScript] vstup: poloměr zatáčky; výstup: maximální rychlost při průjezdu zatáčkou.
   
   
   
2. Stíhací piloti se oprávněně obávají příliš prudkých zatáček. Je-li totiž tělo pilota vystaveno velkému dostředivému zrychlení v situaci, kdy hlava směřuje do středu křivosti zatáčky, dochází k odkrvení mozku a poruše mozkových funkcí. Úplné ztrátě vědomí předchází několik varovných příznaků. Je-li velikost dostředivého zrychlení mezi hodnotami 2g a 3g, cítí se pilot jakoby "těžký". Při hodnotě 4g začíná vidět pouze černobíle a jeho zorný úhel se zmenšuje (tzv. tunelové vidění). Je-li takovému zrychlení vystaven delší dobu anebo se velikost zrychlení dokonce ještě zvětší, přestává pilot vidět úplně a vzápětí ztrácí vědomí. Tento stav se nazývá G-LOC z anglického "gravity-induced loss of consciousness". Jaké je dostředivé zrychlení pilota (v jednotkách g) stíhačky F–22 při průletu kruhové zatáčky o poloměru 5.80 km rychlostí o velikosti v = 2580 km/h?
   
   [JavaScript] vstup: rychlost letadla a poloměr kruhové zatáčky; výstup: velikost dostředivého zrychlení a slovní popis toho, co se s pilotem stane.
   
   Při řešení můžete též využít následující zdroje:
   • The possibility of G-LOC during aerobatics in a light aircraft (Bureau of Air Safety Investigation) [PDF]
   • F-16 accident report released (Oct. 5, 2001) (Air Combat Command)
   • Swissaviation – Ratgeber: Greyout, Blackout und Co.
   • Libelle
   
   
   
3. Because of your knowledge of physics, you have been hired as a consultant for a new James Bond movie, "Oldfinger". In one scene, Bond jumps horizontally off the top of a cliff to escape a villain. To make the stunt more dramatic, the cliff has a horizontal ledge a distance h beneath the top of the cliff which extends a distance L from the vertical face of the cliff. The stunt coordinator wants you to determine the minimum horizontal speed, in terms of L and h, with which Bond must jump so that he misses the ledge.
   
   [JavaScript] input: L and h; output: minimum horizontal speed.
   
   
   
4. Zjistěte, zda ze tří zadaných stran lze sestrojit trojúhelník.
   
   [JavaScript] vstup: délky jednotlivých stran; výstup: zda lze sestrojit trojúhelník.
   
   
   
5. Pro zadanou peněžní částku v korunách určete, kolik je potřeba k výplatě této částky jednotlivých bankovek a mincí. Např. k výplatě 692,60 Kč je třeba 1 x 500 Kč, 1 x 100 Kč, 1 x 50 Kč, 2 x 20 Kč, 1 x 2 Kč, 1 x 50 hal, 1 x 10 hal. Při řešení můžete použít operátor modulo.
   
   [JavaScript] vstup: peněžní částka; výstup: počet jednotlivých bankovek a mincí.
   
   
   

Sada 2

1. Vypište hodnoty polynomu f(n) = n² + n + 41 pro n z intervalu 1 až 100. Pro každou hodnotu f(n) určete, zda jde o prvočíslo. Výstup řešte užitím tabulky.
   
   
2. Vypište n řádků Pascalova trojúhelníku. Jaký je význam Pascalova trojúhelníku? Poté při výpisu barevně odlište sudá a lichá čísla. Následně každé sudé číslo nahraďte při výpisu červenou hvězdičkou a každé liché číslo žlutou hvězdičkou. Jaký geometrický obrazec nyní vznikl?
   
   
3. Divisibility by Seven
   Everyone learns in grade school some simple tests for divisibility by small numbers such as 2, 3, 5, and 9. But far less well-known are some simple divisibility tests for the number 7. Here are a couple:
   • Test #1. Take the digits of the number in reverse order, from right to left, multiplying them successively by the digits 1, 3, 2, 6, 4, 5, repeating with this sequence of multipliers as long as necessary. Add the products. This sum has the same remainder mod 7 as the original number! Example: Is 1603 divisible by seven? Well, 3(1)+0(3)+6(2)+1(6)=21 is divisible by 7, so 1603 is.
   • Test #2. Remove the last digit, double it, subtract it from the truncated original number and continue doing this until only one digit remains. If this is 0 or 7, then the original number is divisible by 7. Example: 1603 –> 160-2(3)=154 –> 15-2(4)=7, so 1603 is divisible by 7.
   The Math Behind the Fact: Here's a hint on how to prove them. For the first test, note that (mod 7), 1==1, 10==3, 100==2, 1000==6, etc. For the second test, note that (mod7), 10A+B==10*(A-2B). The second trick mentioned here can be modified to check for divisibility by other primes. For example, to check divisibility by 13, take the last digit, multiply by 4 and add to the truncated portion. To check divisibility by 19, double the last digit and add. In fact, for any prime p, there exists some integer k such that divisibility by p can be ascertained by multiplying the unit's digit by k and adding (or subtracting) from the truncated portion of the numeral.
   
   
4. Pro zadaný textový řetězec určete, zda jde o palindrom. Palindrom je slovo nebo věta, která se čte stejně zepředu i zezadu (např. KRK, TAHAT, JELENOVI PIVO NELEJ apod.). Pozor na mezery!
   
   
5. Napište funkci pro výpočet druhé odmocniny iterační metodou z nezáporného čísla c:
   x₀ = c (počáteční aproximace),
   x_i+1 = 0.5*(c/x_i+x_i).
   
   
6. Hodnotu Ludolfova čísla π = 3.1415926535897932384626433832795028841971693993751 ···  můžeme spočítat několika iteračními způsoby. Nadefinujte funkce, které spočítají hodnotu Ludolfova čísla podle níže uvedených vztahů. Uživatel musí mít možnost zadat počet iteračních kroků výpočtu.
   
   

   F. Vieta (1540 – 1603)		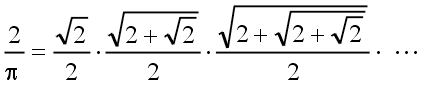(1)
   F. Wallis (1616 – 1703)		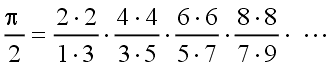(2)
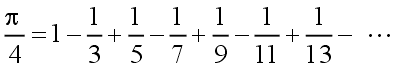
   J. Gregory (1638 – 1675), G. W. Leibniz (1646 – 1716)	neboli	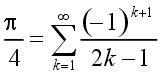(3)
   L. Euler (1707 – 1783)		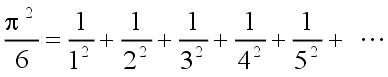(4)
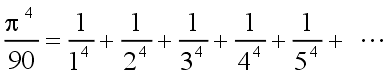   		(5)
   S. Ramanujan (1887 – 1920)		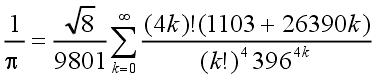(6)