Simulace dynamických systémů v jazyce Java

© Jiří Macur, 2006

5         Agregační diagramy

Již po několika experimentech s našimi programy je vidět, že úplné vyšetření chování konkrétního dynamického systému může být neřešitelným úkolem. Lze ukázat, že pro širokou třídu problémů neexistuje obecná metoda, jak nalézt všechny atraktory nebo všechny pevné body. Situace je však ještě složitější, neboť pro úplné pochopení potřebujeme znát vlastnosti celého souboru dynamických systémů s parametry z co nejširšího spektra přípustných hodnot. V tomto ohledu je stávající teoretické zázemí velmi chudé – analýza se v podstatě omezuje na systémy s jedním parametrem, ostatní možné parametry systému jsou pokládány za konstanty.

5.1        Bifurkační diagram

Z hlediska vizualizace takového souboru systémů je stěžejním nástrojem bifurkační diagram, který zobrazuje závislost typu chování na parametrech systému. Ukážeme si možnou konstrukci bifurkačního diagramu pro náš model buzeného rotátoru. Protože musíme vyjádřit typ chování jedním rozměrem (druhou osu digramu tvoří hodnota parametru), zvolíme hodnoty úhlové rychlosti systému jako reprezentanty chování systému v ustáleném stavu. Navíc vybereme jen hodnoty, které systém nabývá při průchodu Poincarého plochou. Konstrukce diagramu je tedy následující:

1.      Nastavíme hodnotu parametru

2.      Necháme systém vyvíjet tak, až se jeho Poincarého mapa nemění

3.      Vyneseme do grafu hodnoty úhlové rychlosti z Poincarého mapy

4.      Změníme parametr o malou hodnotu

5.      Přejdeme k bodu 2

V bifurkačním diagramu pak bude jednoduchému cyklu odpovídat jeden bod, zdvojenému cyklu dva body, kvaziperiodickému a chaotickému pohybu nespojitá množina bodů. Přestože celý postup působí značně utilitárně, poskytuje výsledný diagram většinou dobrou představu o možném chování systému.

Značným problémem při vytváření diagramu bývá paralelní přítomnost více typů ustáleného chování (více atraktorů při stejném parametru). V podstatě bychom měli náš scénář konstrukce diagramu rozšířit o nalezení ustáleného chování pro všechny počáteční podmínky.

Abychom nepřekročili vymezený rámec tohoto textu, pokusíme se o výrazné zjednodušení uvedeného postupu:

•          ustálení chování dosáhneme konstantní prodlevou mezi nastavením počátečních podmínek a zaznamenáním hodnot v Poincarého mapě,

•          do grafu vyneseme jen konstantní počet hodnot w (v případě jednoduchého cyklu budou ležet v jednom bodě, v případě složitějšího chování však nemusí být celé spektrum možných hodnot zobrazeno),

•          pro každou hodnotu parametru necháme systém ustálit pro několik málo náhodných hodnot počátečních podmínek (méně pravděpodobné atraktory tak nemusí být vůbec viditelné).

Z navrženého postupu je patrné, že vykreslení diagramu je i tak značně náročné na výpočetní zdroje. Při rozumném diskretizačním kroku je pouze velmi malá část vypočtených stavů zobrazována, navíc musíme značnou část hodnot "zahodit" kvůli čekání na ustálení chování.

Proto se při návrhu programu omezíme kvůli jednoduchosti na vlastní konstrukci diagramu a nebudeme se zabývat interaktivními možnostmi vkládání konfiguračních parametrů diagramu. Časová náročnost výpočtu je zkrátka tak vysoká, že pro jinou konfiguraci je zanedbatelná režie nového překladu programu s jinými parametry.

Třída simul bude tedy obsahovat jen dva objekty – jeden s diagramem, druhý s nezávisle se vyvíjejícím rotátorem:

Příklad 5 – bifurkační diagram

Návrh implementace třídy Rotator

 

class Rotator extends Thread                   //dědí funkcionalitu třídy vlákna

{

       public double p;                        //řídicí parametr dyn. systému

       private double q=2, omg=0.6666667;      //zafixované parametry dyn. systému

       private double fi,omega,theta;          //stavové proměnné

       public boolean konec = false;           //indikátor ukončení výpočtu

       private double g = 9.81;                //grav. zrychlení

       private double h = 0.005;               //diskretizační krok

       public Bifur bifur = null;              //reference na zobrazovací diagram

 

       public Rotator()                        //konstruktor

       {

             setState();                       //počáteční podmínky

       }

 

       public void setState()                  //nastaví náhodný nový stav

       {

             fi = Math.PI*(2*Math.random()-1);       // +/- pi

             omega = 5*(2*Math.random()-1);          // +/- 5

             theta = 2*Math.PI*Math.random();        // 0 - 2pi

       }

      

       public double f1(double x1,double x2,double x3)       //definice dyn. systému

       {

             return x2;                       

       }

      

       public double f2(double x1,double x2,double x3)

       {

             return -Math.sin(x1)-x2/q+p*Math.cos(x3);

       }

 

       public double f3(double x1,double x2,double x3)

       {

             return omg;

       }

 

       public void step()                             //výpočet nového stavu

       {

             double h2 = 0.5*h;

      

             double k11 = f1(fi,omega,theta);        //algoritmus Runge-Kutta

             double k12 = f2(fi,omega,theta);

             double k13 = f3(fi,omega,theta);

             double k21 = f1(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k22 = f2(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k23 = f3(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k31 = f1(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k32 = f2(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k33 = f3(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k41 = f1(fi+h*k31,omega+h*k32,theta+h*k33);

             double k42 = f2(fi+h*k31,omega+h*k32,theta+h*k33);

             double k43 = f3(fi+h*k31,omega+h*k32,theta+h*k33);

      

             fi += h/6*(k11+2*k21+2*k31+k41);        //nový stav

             omega += h/6*(k12+2*k22+2*k32+k42);

             theta += h/6*(k13+2*k23+2*k33+k43);

 

             if (Math.abs(fi) >  Math.PI)            //mapovani cyklické proměnné

             {

                    fi -= 2*Math.PI*Math.abs(fi)/fi;

             }

 

             if (theta > 2*Math.PI)                  //mapování fáze

             {

                    theta -= 2*Math.PI;

                    bifur.showState(omega);           //předání bodu do diagramu

             }

       }

      

       public void run()                              //tělo vlákna

       {

             while(!konec)

                    step();

       }

}                                                     //konec třídy Rotator

Návrh třídy se opět příliš neliší od předcházejícího příkladu. Navíc je zde pouze metoda setState(), která nastaví náhodné počáteční hodnoty ve zvoleném rozmezí. V metodě step() je při průchodu Poincarého mapou volána prezentační metoda diagramu showState(), která s výsledkem naloží podle potřeb. Předáváme přitom pouze hodnotu úhlové rychlosti.

Řízení konstrukce diagramu podle výše uvedeného algoritmu svěříme třídě Bifur:

 

class Bifur extends Canvas

{

       private int cInit;                      //čítač pro ustálení chování

       private int cShow;                      //čítač pro počet bodů zobrazení

       private int cStart;                     //čítač pro počáteční podmínky

       private int i = 0;                      //čítač osy x v diagramu

       private int maxInit = 30;               //max. hodnoty čítačů

       private int maxShow = 20;

       private int maxStart = 5;

       private int width,height;               //geometrie oblasti

       private int omega0;                     //střed oblasti v rastrových souřadnicích

       private double minP = 0.5,maxP = 2;     //rozsah řídicího parametru

       private double deltaP;                  //krok řídicího parametru

       public double p;                        //řídicí parametr použije i rotátor

       private double scaleOmega;              //měřítko

       private int omega;                      //stav v rastrových souřadnicích

       private Color fg=Color.black;           //barva popředí

       private Color bg=Color.white;           //barva pozadí

       public Rotator rot=null;                //reference na objekt rotátoru

 

       Bifur(int width0, int height0)          //konstruktor

       {

             super();                          //použije funkcionalitu mateřské třídy

             width = width0;

             height = height0;

             deltaP = (maxP-minP)/width;       //výpočet kroku parametru

             p = minP;                         //nastavení počáteční hodnoty

             omega0 = height/2;                //umístění nulové hodnoty omega

             scaleOmega = (double)omega0/5;    //zobrazovaný interval omega: +/- 5

             this.setSize(width,height);       //nastaví velikost komponenty plátna

       }

 

       public void paint(Graphics g)           //ovladač překreslení

       {

             g.setColor(fg);

             setBackground(bg);

             g.drawString("Bifurkační diagram 1",10,15);

       }

 

       public int y(double omega)              //transf. úhlové rychlosti

       {                                       //do rastrového zobrazení

             return (int)(omega0+scaleOmega*omega);

       }

 

       public void showState(double o)                //zobrazení stavu vyvolá rotátor

       {                                              //při průchodu Poinc. rovinou

             if(cInit++ < maxInit) return;            //počkáme na ustálení

             if(cShow++ < maxShow)                   //zobrazí potřebný počet bodů

             {

                    Graphics g = this.getGraphics();  //získání grafického kontextu

                    g.setColor(fg);                   //nastavení barvy

                    omega = y(o);                     //transf. stavu do nových souř.

                    g.drawLine(i,omega,i,omega);      //vykreslení bodu v diagramu

                    return;

             }

             cInit = 0; cShow = 0;                   //vynulujeme čítače

             if(cStart++ < maxStart)                 //čítač počtu nastavení poč. podm.

             {

                    rot.setState();                   //nastavení nových náhod. hodnot

                    return;

             }

             cStart = 0;                             //zobrazování ukončeno

             if(p < maxP)                            //až do konce diagramu

             {

                    p += deltaP; i++;                 //změníme hodnotu parametru o krok

                    rot.p = p;                        //předáme ho rotátoru

                    return;

             }

       }

}

Návrh třídy nepotřebuje příliš dalších komentářů. Jejím jádrem je metoda showState, kterou vyvolá rotátor vždy, když jeho trajektorie prochází Poincarého rovinou (slouží tedy jako ovladač této události rotátoru). V metodě je realizován výše uvedený postup, kdy po ustálení stavu vynášíme několik hodnot úhlové rychlosti, nastavíme několikrát počáteční podmínky a poté změníme řídicí parametr.

Návrh implementace třídy simul

 

public class simul extends Applet

{

       private Bifur bifur;

       private Rotator rot;

      

       public void init()                      //inicializace appletu ("konstruktor")

       {

             setLayout(new FlowLayout());

             bifur = new Bifur(600,300);       //vytvoří instanci diagramu

             add(bifur);                       //zařadí ho do správy plochy

             bifur.repaint();                  //vynutí překreslení

 

             rot = new Rotator();              //vytvoří instanci objektu rotátor

 

             rot.bifur = this.bifur;           //předá vzájemné odkazy

             rot.p = bifur.p;                  //poč. hodn. parametru je v obj. bifur

             bifur.rot = this.rot;

 

             rot.start();                      //spustí tělo vlákna rotátoru

       }

      

       public void stop()                      //konec appletu ("destruktor")

       {

             rot.konec = true;                 //konec vlákna rotátoru

             super.stop();                     //dokončí destrukci mateřskou třídou

       }

}

Implementace je velmi jednoduchá. Již jsme uvedli, že se nebudeme zabývat žádným interaktivním nastavováním konfigurace diagramu. Třída tedy neobsluhuje žádné události, pouze spustí potřebné objekty a nastaví jim potřebné reference.

Ve třídě Bifur je nastavena následující konfigurace:

Parametry q = 2, W = 2/3, rozsah řídicího parametru 0.5 < p < 2.

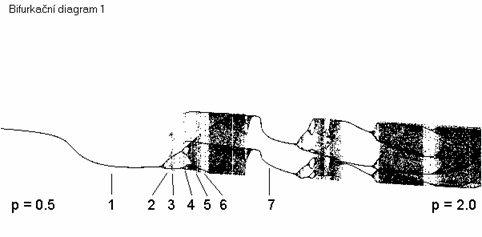Obr. 5.1. Vykreslený bifurkační diagram podle programu 5

Spustit program 5

V diagramu jsme označili několik oblastí:

1 – Oblast jednoduchého ustáleného cyklu

2 – Oblast zrození dvou jednoduchých cyklů (jeden atraktor se štěpí na dva). Rozštěpení (bifurkace – vidlička) je generický jev, který se v různých variantách v diagramu opakuje – odtud jeho název.

3 – Nedokonale zobrazená přítomnost málo přitahujícího dalšího atraktoru.

4 – Zdvojení periody obou atraktorů – jiný příklad bifurkace

5 – Kaskádové zdvojování period vede až k chaotickému chování

6 – V oblasti chaotického chování se vyskytují "okna" regulárního chování. Jejich  rozmístění má fraktálový charakter, tj. vyskytují se hustě s různou šířkou. Uvedené okno obsahuje stabilní cyklus se ztrojenou periodou, která indikuje vždy chaotické chování v blízkém okolí okna.

7 – Postupné "interakce" dalších atraktorů vedou až k jejich "anihilaci" a ke vzniku dvou velmi stabilních jednoduchých cyklů. V dalších oblastech dojde k jejich dalším bifurkacím a novým oblastem chaotického chování.

Návrh našeho programu umožňuje snadnou možnost potlačení ustalovacího procesu – stačí nastavit konstantu maxInit = 0. V bifurkačním diagramu pak vidíme rozmazané motivy, z kterých si lze udělat obrázek o "hustotě stavů" při různých hodnotách parametru nerovnovážného systému. Diagram má určitou vypovídající hodnotu i o stabilitě atraktorů a jejich přitažlivosti. Celá nerovnovážná problematika je však ještě méně teoreticky zpracována než v případě ustáleného chování.

Obr. 5.2. Vyjádření přechodových dějů v bifurkačním diagramu

Úkoly a náměty:

•          V kombinaci s programem 4 zkoumejte konkrétní tvary atraktorů v různých oblastech bifurkačního diagramu. Zaměřte se zejména na okolí dramatických změn (např. bifurkačních bodů nebo prudkých změn tvaru atraktorů).

•          Návrh implementace našeho programu by bylo možné výrazně zefektivnit zejména pomocí cíleného vyhodnocení ustáleného stavu a zobrazování násobných bodů v Poincarého mapě (nemuseli bychom čekat zbytečně dlouho na ustálení ani vykreslovat body jednoduchých cyklů zbytečně "přes sebe"). Návrh takového algoritmu již ponecháváme čtenáři, upozorňujeme však, že nemusí být nijak jednoduchý.

•          Velmi zajímavé by bylo rovněž provést dostatečně husté rozmítání počátečních podmínek při každé hodnotě parametru a barevně odlišit, kolikrát padlo ustálení do stejného bodu. Bifurkační diagram by potom poskytoval i informaci o přitažlivosti zobrazovaných atraktorů. Je však zřejmé, že taková úloha by byla extrémně náročná na výpočetní čas – pak by bylo vhodnější použít nejen velmi silný počítač, ale i kompilovaný jazyk.

•          Dalším (tentokrát snadno dosažitelným) experimentem může být vizualizace vývoje málo přitažlivých atraktorů. Již bylo řečeno, že některé atraktory jsou málo pravděpodobné ve smyslu malé množiny počátečních podmínek, které jsou jimi přitahovány. Příkladem takového atraktoru je ztrojený cyklus přítomný v oblasti 2, kde dominují dva jednoduché cykly (např. pro hodnotu parametru p = 1.028, s počátečními podmínkami j = 3.06, w=0.56, q=0, které lze nalézt pomocí příkladu 4). Pokud se nám podaří "posadit" systém do uvedeného cyklu, můžeme ho nechat vyvíjet bez vnější změny počátečních podmínek, pouze s pomalou změnou řídicího parametru. Systém se udrží v tomto typu cyklu přes několik bifurkačních bodů, poté přejde spontánně na některý z dominantních atraktorů. Při větší změně parametru však systém vypadne z málo stabilního atraktoru dříve (viz obr. 5.3)

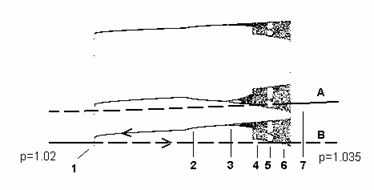Obr. 5.3. Detail oblasti 3 bifurkačního diagramu z obr. 5.1.

Uvedený námět je rozpracován na výše uvedeném obrázku. Chceme-li zachytit celý vývoj málo stabilního atraktoru, musíme v programu potlačit změnu počátečních podmínek a navíc musíme diagram konstruovat ze zvoleného počátku dvěma směry. Cyklus s trojitou periodou má určitá specifika, která jsou analyticky intenzivně zpracovávána. Zde opět pouze popíšeme typické oblasti trvání cyklu:

1 – Bod (hodnota parametru), kde cyklus spontánně skokem zaniká (katastrofický přechod) a chování přechází do jednoduchého cyklu B. Zrod cyklu vykazuje výraznou hysterezi: pokud měníme (zvyšujeme) hodnotu parametru opačným směrem, cyklus nevzniká nejen v tomto bodě, ale  neobjeví se vůbec.

2 – Oblast relativně stabilního cyklu se ztrojenou periodou.

3 – Bifurkace typu zdvojení periody. Výsledný cyklus je šestinásobný.

4 – Oblast chaotického chování, které se rozvine po rychlé kaskádě dalších bifurkací.

5 – Okno regulárního chování. V každé větvi se opět zrodí cykly s trojitou periodou.

6 – Další rozvinutí zdvojení period vede k novému chaotickému chování,

7 – Cyklus opět skokem zaniká, chování je přitaženo dominantním jednoduchým cyklem A.

5.2        Oblasti přitažlivosti

Již bylo zmíněno, že pro určité hodnoty parametrů systému existuje současně více atraktorů různých typů. V systému může být přítomen chaotický atraktor spolu s jednoduchým cyklem nebo několik cyklů s různým počtem zdvojení periody, resp. kvaziperiodických atraktorů. Nejen, že neexistuje obecný algoritmus, jak nalézt všechny atraktory v systému, ale není k dispozici také žádný postup, kterým bychom mohli při nalezené množině atraktorů vyloučit přítomnost dalšího atraktoru (např. s velmi malou přitažlivostí). Pro jednoduché systémy však lze pro speciální hodnoty parametrů s dostatečně velkou pravděpodobností nalézt všechny atraktory, zejména pokud jsou tvořeny jednoduchými cykly. Tuto možnost využijeme pro nalezení tzv. oblastí (bazénů) přitažlivosti.

Oblast přitažlivosti atraktoru je tvořena množinou počátečních podmínek (bodů ve fázovém prostoru), z nichž systém konverguje k danému atraktoru.

Prakticky vypadá konstrukce oblastí přitažlivosti následovně:

1.      vybereme podmnožinu fázového prostoru,

2.      rozdělíme ji do pravoúhlého rastru,

3.      z každé buňky rastru vybereme jeden bod, do něhož položíme počáteční podmínku,

4.      necháme systém vyvíjet až do ustálení,

5.      identifikujeme atraktor, v němž se systém ustálil,

6.      vybarvíme celou buňku barvou specifickou pro tento atraktor.

Určitým problémem jsou body 4 a 5. Při obecném atraktoru je zjištění ustálení obtížný problém, stejně tak může být nesnadné zjistit, o jaký atraktor se jedná.

Pro konkrétní jednoduchý systém si však můžeme situaci značně usnadnit. Například pokud víme, že existují pouze dva atraktory v podobě jednoduchého cyklu, můžeme experimentálně zjistit agregační koeficient, kterým se oba cykly dostatečně liší (např. hodnotu některé stavové složky, velikost stavového vektoru apod.). Pak stačí testovat při každém průchodu Poincarého rovinou, "vzdálenost" stavu od uvedeného agregátu obou atraktorů. Při hodnotě menší než zvolená odchylka zastavíme další testování, vybarvíme buňku rastru a přejdeme na jinou.

V konkrétní implementaci ztotožníme buňky rastru s jednotlivými pixely v zobrazované oblasti.

Vzhledem k tomu, že výpočet je opět časově značně náročný, i tentokrát rezignujeme na interaktivní ovlivňování programu uživatelem, potřebnou konfiguraci vložíme přímo do hodnot atributů navrhovaných tříd.

Vyšetříme oblasti přitažlivosti pro dva jednoduché cykly v oblasti 7 bifurkačního diagramu na obr. 5.1. Pomocí programu 4 (např. do metody showState() třídy Mapa vložíme kontrolní výstup System.out.println(fi+","+omega)) snadno zjistíme, že pro koeficient p=1.35 dostáváme pro každý z cyklů při průchodu Poincarého rovinou stav s následujícími hodnotami j=0.88, w=1.91, resp. j = –0.045, w=0.76.

Ustálení systému budeme testovat triviálním způsobem: hodnoty parametru j ve dvou následujících průchodech Poincarého rovinou splňují podmínku  |j₁ - j₂| < e, kde e je malá konstanta.

Z uvedených hodnot ustálení je patrné, že se jednotlivé cykly liší např. znaménkem hodnoty j.

Příklad 6 – bazény přitažlivosti

Návrh implementace třídy Rotator

class Rotator extends Thread                   //dědí funkcionalitu třídy vlákna

{

       private double p=1.35, q=2, omg=0.6667; //konstantní parametry dyn. systému

       private double fi,omega,theta;          //stavové proměnné

       public double fi0 = 0, omega0 = 0;      //počáteční hodnoty se mění z vnějšku

       public boolean zmena = false;           //indikátor změny počátečních podmínek

       public boolean konec = false;           //indikátor ukončení výpočtu

       private double g = 9.81;                //grav. zrychlení

       private double h = 0.005;               //diskretizační krok

       public Basen basen = null;              //reference na zobrazovací diagram

 

       public Rotator()                        //konstruktor

       {

             fi = fi0; omega = omega0;         //počáteční podmínky

       }

 

       public void setState()                  //nastaví nespojitý nový stav

       {

             if (zmena)

             {

                    fi = fi0;

                    omega = omega0;

                    theta = 0;

                    zmena = false;

             }

       }

      

       public double f1(double x1,double x2,double x3)       //definice dyn. systému

       {

             return x2;                       

       }

      

       public double f2(double x1,double x2,double x3)

       {

             return -Math.sin(x1)-x2/q+p*Math.cos(x3);

       }

 

       public double f3(double x1,double x2,double x3)

       {

             return omg;

       }

 

       public void step()                                    //výpočet nového stavu

       {

             double h2 = 0.5*h;

      

             double k11 = f1(fi,omega,theta);               //algoritmus Runge-Kutta

             double k12 = f2(fi,omega,theta);

             double k13 = f3(fi,omega,theta);

             double k21 = f1(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k22 = f2(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k23 = f3(fi+h2*k11,omega+h2*k12,theta+h2*k13);

             double k31 = f1(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k32 = f2(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k33 = f3(fi+h2*k21,omega+h2*k22,theta+h2*k23);

             double k41 = f1(fi+h*k31,omega+h*k32,theta+h*k33);

             double k42 = f2(fi+h*k31,omega+h*k32,theta+h*k33);

             double k43 = f3(fi+h*k31,omega+h*k32,theta+h*k33);

      

             fi += h/6*(k11+2*k21+2*k31+k41);               //nový stav

             omega += h/6*(k12+2*k22+2*k32+k42);

             theta += h/6*(k13+2*k23+2*k33+k43);

 

             if (Math.abs(fi) >  Math.PI)            //mapovani cyklické proměnné

             {

                    fi -= 2*Math.PI*Math.abs(fi)/fi;

             }

 

             if (theta > 2*Math.PI)                  //mapování fáze

             {

                    theta -= 2*Math.PI;

                    basen.showState(fi);              //zobrazení bodu v diagramu

             }

       }

      

       public void run()                              //tělo vlákna

       {

             while(!konec)

             {

                    setState();                       //test na nový počátek

                    step();

             }

       }

}

Ve třídě jsou pevně nastaveny parametry, počáteční podmínky jsou nastavovány zvnějšku. Při průchodu trajektorie Poincarého rovinou předáváme v metodě step() hodnotu vnitřní stavové proměnné fi, která slouží jak pro test ustálení, tak identifikaci konkrétního atraktoru. Návrh třídy se proti předcházejícímu příkladu 4 téměř nezměnil.

Návrh implementace třídy Basen

 

class Basen extends Canvas

{

       private int width,height;               //geometrie oblasti

       private int x,y;                        //čítače pro jednotlivé buňky rastru

                                               //vyšetřovaná podmnožina fáz. prostoru

       private double minFi = -Math.PI, maxFi = Math.PI;

       private double minOmega = -10, maxOmega = 10;

 

       private double deltaFi, deltaOmega;     //krok pro počáteční podmínky

       private double fi,omega;                //poč. podmínky pro rotátor

       private double oldFi,eps = 0.01;        //proměnné pro test ustálení

 

       private Color fg=Color.black;           //barva popředí

       private Color bg=Color.white;           //barva pozadí

       public Rotator rot=null;                //reference na objekt rotátoru

 

       Basen(int width0, int height0)          //konstruktor

       {

             super();                          //použije funkcionalitu mateřské třídy

             width = width0; height = height0;

             x = y = 0;                        //vynulujeme rastrové čítače

             fi = minFi; omega = minOmega;     //startovací podmínky pro rotátor

             deltaFi = (maxFi-minFi)/width;    //kroky poč. podmínek

             deltaOmega = (maxOmega-minOmega)/height;

 

             this.setSize(width,height);       //nastaví velikost komponenty plátna

       }

 

       public void paint(Graphics g)           //ovladač překreslení

       {

             g.setColor(fg);

             setBackground(bg);

       }

 

       public void setStart()                  //nastaví rotátoru nové poč. podmínky

       {

             rot.fi0 = fi;                     //nové hodnoty v objektu rotátoru

              rot.omega0 = omega;

             rot.zmena = true;                 //informuje o změně

       }

       public void showState(double rotFi)            //zobrazení stavu vyvolá rotátor

       {

             if(((oldFi+eps) > rotFi) && ((oldFi-eps) < rotFi))    //čekáme na ustálení

             {

                    if (rotFi > 0)                          //rozlišení typu cyklu

                    {

                           Graphics g = this.getGraphics();

                           g.setColor(fg);                   //nastavení barvy

                           g.drawLine(x,y,x,y);              //vykreslení bodu v diagramu

                    }

                    if (++x > (width-1))                    //posun v rastru

                    {

                           x=0;                              //nový řádek

                           if(y < height) y++;

                    }

                    fi = minFi + x*deltaFi;                 //nové poč. podmínky

                    omega = minOmega + y*deltaOmega;

                    setStart();                             //nastavíme rotátor

             }

             else oldFi = rotFi;                            //ještě neustáleno

       }

}

Vidíme, že návrh zobrazovací třídy je opět velmi přímočarý. Jádrem třídy je metoda showState, kterou vyvolá rotátor při průchodu trajektorie Poincarého rovinou. Zároveň předá metodě hodnotu stavové proměnné.

V metodě nejdříve testujeme, zda došlo k ustálení (hodnota eps=0.01 byla zvolena tak, aby s dostatečnou redundancí zaručovala, že z daného stavu se systém již nemůže dostat do jiného typu cyklu).

Po ustálení rozlišíme typ cyklu (znaménkem stavové proměnné), v případě jednoho typu cyklu zobrazíme pixel, v druhém případě ponecháme barvu pozadí.

Přesuneme se na další buňku v rastru, vypočítáme novou hodnotu počátečních podmínek, které buňka reprezentuje, a podmínky předáme rotátoru.

Návrh implementace třídy simul

 

public class simul extends Applet

{

       private Basen basen;

       private Rotator rot;

      

       public void init()                      //inicializace appletu ("konstruktor")

       {

             setLayout(new FlowLayout());

             basen = new Basen(300,300);       //vytvoří instanci oblasti přit.

             add(basen);                       //zařadí do správy plochy

             basen.repaint();                  //vynutí překreslení

 

             rot = new Rotator();              //vytvoří instanci objektu rotátor

 

             rot.basen = this.basen;           //předá vzájemné odkazy

             basen.rot = this.rot;

             basen.setStart();                 //nastaví startovací poč. podmínky

 

             rot.start();                      //spustí tělo vlákna rotátoru

       }

      

       public void stop()                      //konec appletu ("destruktor")

       {

             rot.konec = true;                 //konec vlákna rotátoru

             super.stop();                     //dokončí destrukci mateřskou třídou

       }

}

Implementace třídy již v této fázi snad nevyžaduje žádný komentář.

Připomeňme, že výsledné zobrazení oblastí přitažlivosti vychází z této konfigurace:

p = 1.35, jÎ <–p, p >,  wÎ <–10, 10 >

Obr. 5.4. Bazény přitažlivosti dvou jednoduchých cyklů a detail hranic přitažlivosti

Spustit program 6

Vidíme, že oblasti jsou do sebe vnořeny složitým apůsobem, zejména na hranicích oblastí není snadné určit, kam vlastně systém konverguje. Ve skutečnost lze ukázat, že uvedené hranice mají fraktálový charakter, jsou tedy "nekonečně členité". Pro ilustraci je zobrazen také detail naznačený v původním obrázku. Je zřejmé, že detail je stejně "složitý" jako původní obrázek a že další detail z detailního záběru by rovněž nepřinesl žádnou změnu (ve skutečnost detailnější zkoumání hranic přitažlivosti přináší určitý problém – systém se v okolí hranic pomaleji ustaluje a náš program tedy vykresluje hranice mnohem pomaleji).

Modifikujme nyní program 6 tak, aby zobrazoval bazény přitažlivosti v oblasti 2 bifurkačního diagramu na obr. 5.3. Program musí rozlišit tři druhy atraktorů: dva jednoduché cykly a jeden méně pravděpodobný cyklus s trojitou periodou. Experimentálně zjištěné hodnoty stavu při průchodu Poincarého rovinou (pomocí programu 4) pro uvedené druhy cyklů jsou:

Parametry: p = 1.028, q = 2, W = 2/3

Rozlišit typ cyklu můžeme opět pomocí jediné stavové proměnné j např. takto:

cyklus A: j  < –1        cyklus B: j  < –0.3     cyklus C: ostatní případy

Problémem však zůstává indikace ustálení. Nelze totiž beze změny převzít mechanizmus s příkladu 6, neboť pro cyklus C jsou dva po sobě jdoucí body vždy různé. Nejjednodušší (i když nikoli nejefektivnější) metodou je tedy použít pro porovnání pouze každý třetí bod. U jednoduchých cyklů se tímto trikem nic nezmění (v ustálení jsou všechny průchody Poincarého rovinou totožné), u cyklu C však zajistíme porovnávání odpovídajících větví trojného cyklu. Při vykreslování musíme rozlišit cykly třemi alternativními barvami. Vzhledem k jemným motivům ve výsledném diagramu je třeba volit značně kontrastní barvy, např. černá, červená, bílá.

Uvedené zásahy do programu jsou tak triviální, že je ponecháváme na čtenáři.

          

Obr. 5.5. Oblasti přitažlivosti při přítomnosti tří limitních cyklů a detail oblastí

Úlohy:

•          Pokuste se navrhnout obecný algoritmus, který by nevyžadoval experimentální zjišťování ustálených podmínek a byl by schopen rozlišit a znázornit oblasti přitažlivosti libovolného počtu atraktorů. Zkonstruovat uvedený algoritmus je poměrně snadné, pokud se nejedná o kvaziperiodické nebo chaotické chování, které tedy musíme, bohužel, vyloučit.

•          Pokuste se o zmapování vývoje oblastí přitažlivosti pro určitý interval parametru p (např. oblasti 2 bifurkačního diagramu na obr. 5.1). Působivá je zejména animace vývoje oblastí přitažlivosti, která poskytuje poměrně hluboký vhled do chování systému.

 

Obsah