7 Numerické metody
počáteční úloha
diskretizace proměnných
uzly sítě
diferenční metody
krok metody
jednokrokové metody
Eulerova metoda
řád metody
metody Runge-Kutta
vícekrokové metody
implicitní a explicitní metody
samostartovací metody
Adams-Bashfothova a Adams-Moultonova metoda
prediktor, korektor
krokové a globální chyby výpočtu7.1 Numerická metoda Runge-Kutta
7.2 Stoermerova formule a metody GBS
7.3 Vícekrokové Adamsovy metody
7.4 Algoritmus prediktor-korektor
7.5 Odhad chyby výpočtu
Při simulaci dynamických systémů reprezentovaných soustavou diferenciálních rovnic (2.2) se používá řada numerických metod, vyvíjených od počátku tohoto století. Metody lze rozčlenit podle mnoha kriterií do různých tříd a studovat přitom jejich efektivitu z hlediska přesnosti a numerické náročnosti. Šíře teorie v této oblasti často odrazuje od použití numerických metod v běžné praxi, proto se zde seznámíme pouze s jednoduššími postupy, které postačí na simulaci demonstrovaných soustav (je třeba poznamenat, že pro chaotické systémy stejně každá metoda dříve nebo později selže v tom smyslu, že pro každou přesnost existuje konečný čas, po kterém je požadovaná tolerance překročena).
Uvažujme nejprve nejjednodušší systém s jedinou stavovou proměnnou (fázovým prostorem je přímka R):
| (7.1) |
s počáteční podmínkou x(t0)=x0, jehož řešením je trajektorie x=x(t). Protože se jedná o nalezení trajektorie splňující počáteční podmínku zadávanou obvykle definicí stavu systému v čase t0, nazývá se uvedený problém počáteční úloha.
U většiny praktických úloh nelze nalézt analytické řešení, proto je třeba trajektorii hledat numerickou metodou. Základním principem numerického řešení je obvykle diskretizace proměnných, kdy řešení (spojitou trajektorii) nahradíme posloupností diskrétních bodů
x0(t0), x1(t1), x2(t2), ... , kde t0 < t1 < t2 < ...
Hodnoty nezávisle proměnné t tvoří tzv. uzly sítě. Pokud budou body posloupnosti dostatečně husté, lze je považovat za přibližnou reprezentaci hledané trajektorie. Uvedené metody se nazývají diferenční. Vzdálenost mezi dvěma sousedními body sítě
| (7.2) |
se nazývá krok metody a nemusí být obecně konstantní (síť není ekvidistantní), avšak my budeme používat metody výhradně s konstantním krokem (hi= h). Nezávisle proměnnou v našich systémech je totiž vždy čas a při simulaci (tj. nalezení a zobrazení nového stavu systému) potřebujeme, aby byl čas homogenní, neboť pak zobrazíme správně i rychlost vývoje systému.
Nový stav systému v čase ti vždy počítáme na základě předcházejích stavů systému v čase ti-1, ti-2 , ... , ti-k. Pokud je k =1 hovoříme o jednokrokové metodě, tj. nový stav systému odvodíme z předcházejícího stavu.
Nejjednodušším představitelem jednokrokových metod je Eulerova metoda, kde nový stav lze stanovit z předcházejícího na základě vztahu
| (7.3) |
Uvedený vztah lze jednoduše odvodit dvěma způsoby:
1. Nahrazením vztahu (7.1) diferenčním vztahem
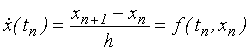 |
(7.4) |
odkud ihned plyne Eulerův vztah
2. Taylorův rozvoj v okolí bodu xn= x(tn) lze vyjádřit řadou
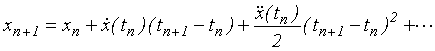 |
(7.5) |
což pro ekvidistantní síť dává po dosazení z (7.1)
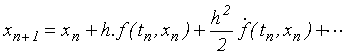 |
(7.6) |
Vidíme, že Eulerův vztah je lineární aproximací Taylorova rozvoje.
Protože je funkce f(x,t) ohraničená včetně všech svých derivací (systém by v žádném stavu neměl mít nekonečnou rychlost, zrychlení apod.), je Eulerův vztah přibližný s chybou úměrnou druhé mocnině kroku h (tzv. diskretizační chyba metody je O(h2), což znamená, že pro dostatečně malý krok je chyba odhadu nového stavu |en|< Ch2, kde C je konstanta). Metoda s chybou O(h2) je tzv. metoda prvního řádu (obecně pro chybu kroku O(hp) je metoda řádu p-1).
Eulerova metoda je v praxi obvykle nepoužitelná. Vypočtený nový stav odpovídá skutečnosti jenom při konstantní rychlosti systému (viz obr.7.1), při každém zakřivení trajektorie (zrychlení), přejdeme při Eulerově metodě na jinou blízkou trajektorii.
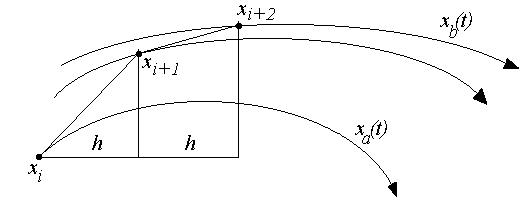
Obr.7.1 Geometrická interpretace Eulerovy metody. Nový bod xi+1 leží ve směru tečny v bodě xi ke skutečné trajektorii x(t). Po dvou krocích způsobí chyba metody přechod z trajektorie xa(t)na xb(t).
7.1 Numerická metoda Runge-Kutta
Vychází opět z Taylorova rozvoje a bere do úvahy i členy vyšších řádů. Potřebné derivace funkce f(t,x) počítá složitější diferenční metodou pomocí dalších pomocných bodů mezi sousedními uzly v síti. Metod Runge-Kutta je více, nejoblíbenější je tzv. klasická metoda 4. řádu, která pro naše potřeby postačí. Vyjádření nového stavu systému pomocí předcházejícího stavu je dáno vztahy:
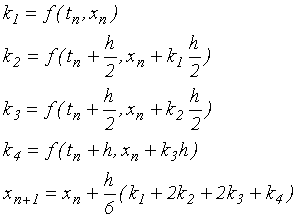 |
(7.7) |
Pomocné hodnoty ki představují derivace stavu (rychlosti) systému ve speciálních bodech na začátku, konci a uprostřed intervalu <tn , tn+1>.
Poznámka:
Diskretizační chyba metody je O(h5), tedy pro krok h=0.1 je chyba řádu 10-5.
Pro dosažení stejné přesnosti bychom museli v rozmezí kroku h vykonat 1000 mezikroků
Eulerovou metodou. Takové úvahy je ovšem třeba brát s rezervou, neboť skutečná
chyba závisí na složitosti reálné trajektorie a odhad chyby nic neříká o
ohraničující konstantě C (viz výše).
V případě fázového prostoru vyšší dimenze m (m>1) je stav systému popsán vektorem x a dynamický systém vektorovou funkcí f(t,x). Algoritmus Runge-Kutta je pak třeba psát ve vektorové formě, tj. pomocné hodnoty ki budou nyní m-složkové vektory, takže např. vztah v (7.7) k1= f (tn , xn) tvoří soustavu rovnic:
Klasická metoda Runge-Kutta nepatří k nejmodernějším, ale dosud se často používá, i když se pro přesnější výpočet příliš nehodí. Populární je také adaptivní metoda Runge-Kutta, kdy se vypočítá nový stav pomocí jednoho a následně podruhé pomocí více kroků, a pokud diference výsledků překračuje zadanou toleranci, dělení sítě se zjemní. Při animaci však tuto metodu použít nemůžeme, neboť potřebujeme pro výpočet nového stavu vždy stejný čas výpočtu pro znázornění odpovídající rychlosti.
7.2 Stoermerova formule a metody GBS
Pro srovnání zde připomeneme velmi starou numerickou metodu (1907), kterou lze použít pro řešení počátečních úloh pro konzervativní dynamické systémy definované diferenciální rovnicí druhého řádu:
| (7.8) |
s počátečními podmínkami
Vztah (7.8) je obvykle přímo pohybová rovnice simulovaného systému. Místo obvykle doporučovaného přeformulování rovnice (7.8) do soustavy rovnic prvního řádu (př.2.1), lze použít Stoermerovu formuli, založenou na rozdělení diskretizačního intervalu H na m ekvidistantních podintervalů h. Zde použijeme Henricim modifikovaný tvar formule pro zmenšení zaokrouhlovací chyby:
Pro i = 1,2,..,m-1
Výsledný nový stav po kroku H je pak dán dvojicí xm,vm, kde
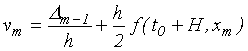 |
(7.9) |
Formule tvoří metodu 2. řádu a lze ji použít přímo na pohybové rovnice systému. Metoda není přesná, ale je velmi stabilní, a někdy se proto používá pro simulaci vícečásticových soustav. Pro fázový prostor vyšší dimenze n (n>1) je opět nutné přeformulovat algoritmus do vektorové podoby (srov. metodu Runge-Kutta), kde pomocné hodnoty Di jsou vektory a funkce f(t,x) je rovněž vektorová.
Obdobné metody dělení základního kroku se nazývají souhrnně modifikované
obdélníkové pravidlo a používají se v souvislosti s velmi efektivní metodou
GBS (Gragg, Bulirsch, Stoer). Podstatou této metody je výpočet nového stavu v
několika verzích pro různé dělení základního kroku H. Výsledná
posloupnost stavů pro různá m se pak extrapoluje (např. Richardsonovou
extrapolační metodou) pro ![]() , což
odpovídá nekonečně jemnému dělení základního intervalu.
, což
odpovídá nekonečně jemnému dělení základního intervalu.
7.3 Vícekrokové Adamsovy metody
Vícekrokové metody používají k vyjádření nového stavu systému znalost k předcházejících stavů. Obecně nelze říci, že vícekroková metoda je nutně efektivnější než jednokroková. Avšak za předpokladu spojitého systému, který se nevyvíjí příliš dramaticky, je pravděpodobné, že odhad nového stavu bude přesnější. Pokud odhlédneme od paměťových nároků metody (nutnost uložení více stavů), obecně neroste výpočetní složitost s počtem kroků k. Nový stav systému vyjádříme obecně pomocí vztahu (tzv. lineární k-kroková metoda):
| (7.10) |
kde ai a bi jsou vhodné konstanty. Je-li konstanta
b0ą0, je nový stav systému závislý
na neznámé hodnotě funkce
| (7.11) |
kde konstanty bi závisí na počtu kroků k a pro k<6 jsou uvedeny v tabulce tab.7.1. Řád metody odpovídá počtu kroků, k výpočtu nového stavu je třeba mít k dispozici k předcházejících stavů. Při startu metody se tyto počáteční stavy zjišťují např. metodou Runge-Kutta (z tohoto důvodu se nazývají jednokrokové metody též samostartovací).
Tab. 7.1 Koeficienty Adams-Bashforthovy metody
| k | 1 | 2 | 3 | 4 | 5 | řád |
| bi | 1 | 1 | ||||
| 2 bi | 3 | -1 | 2 | |||
| 12 bi | 23 | -16 | 5 | 3 | ||
| 24 bi | 55 | -59 | 37 | -9 | 4 | |
| 720 bi | 1901 | -2774 | 2616 | -1274 | 251 | 5 |
Stejným postupem nahrazení trajektorie polynomem, avšak s připuštěním neznámé hodnoty fn+1, dostáváme po numerické integraci (7.1) tzv. Adams-Moultonův vztah
| (7.12) |
kde konstanty ![]() rovněž závisí na
počtu kroků k a pro k<6 jsou uvedeny v tabulce tab.7.2. Vidíme, že
pro k kroků je metoda řádu k+1, její důležitou předností je kromě
toho vyšší stabilita, avšak problémem je nalezení neznámé hodnoty fn+1.
rovněž závisí na
počtu kroků k a pro k<6 jsou uvedeny v tabulce tab.7.2. Vidíme, že
pro k kroků je metoda řádu k+1, její důležitou předností je kromě
toho vyšší stabilita, avšak problémem je nalezení neznámé hodnoty fn+1.
Tab. 7.2 Koeficienty Adams-Moultonovy metody
| k | 0 | 1 | 2 | 3 | 4 | řád |
| b'i | 1 | 1 | ||||
| 2 b'i | 1 | 1 | 2 | |||
| 12 b'i | 5 | 8 | -1 | 3 | ||
| 24 b'i | 9 | 19 | -5 | 1 | 4 | |
| 720 b'i | 251 | 646 | -264 | 106 | -19 | 5 |
7.4 Algoritmus prediktor-korektor
Problém výpočtu neznámé hodnoty fn+1 ve vztahu (7.12) iteračním postupem lze vyjádřit vztahem
| (7.13) |
kde hodnota s+1xn+1 vyjadřuje s+1 iteraci a člen g je v iteračním vztahu konstantní (reprezentuje explicitní část metody).
Lze ukázat, že pro spojitou a omezenou funkci f, uvedená metoda postupných aproximací vždy konverguje. Účinnost metody závisí mimo jiné na výběru prvního odhadu stavu 0xn+1. Algoritmus prediktor-korektor používá pro první odhad Adams-Bashforthovu metodu pokud možno stejného řádu, jako je následně použitá implicitní metoda. První odhad explicitní metodou se nazývá prediktor (P), jeden krok iterace se skládá z výpočtu funkce f (evaluace - E) a následné opravy nového stavu podle vztahu (7.13), tzv. korektor (C). Pro n iterací se obecně metoda značí P(EC)n. Teorie ukazuje, že z hlediska efektivity algoritmu obvykle postačuje n<3. Stabilitu metody lze zvýšit dalším vyčíslením funkce f při konečně stanovené hodnotě xn+1. Tento nejčastěji použitý tvar algoritmu se označuje P(EC)nE. Pro simulaci systémů, kde jsou jednokrokové metody Runge-Kutta již zjevně neefektivní, budeme používat algoritmus typu PECE, který má největší oblast stability.
Celkový algoritmus má tedy následující kroky:
7.5 Odhad chyby výpočtu
Chyby numerických metod se zásadně dělí na krokové a globální (chyby vznikající kumulací chyb v jednotlivých krocích). Obecně platí, že je-li diskretizační chyba řádu O(hp), pak globální chyba je O(hp-1), detailní teorie je však značně složitá. Chybu lze v době výpočtu sledovat např. srovnáváním výsledků při zvýšení hustoty diskretizačních bodů, musíme však mít jistotu, že použitá metoda konverguje. Jinou možností je srovnávat výsledek s očekávaným chováním vyplývajícím ze známých zákonitostí simulovaného systému (např. symetrie). Při simulaci konzervativních dynamických systémů máme jednoduchou možnost přímého sledování chyby výpočtu. Chyba, které se dopustíme při výpočtu nového stavu totiž způsobí, že se v novém stavu přesuneme na jinou blízkou trajektorii, odpovídající jiným počátečním podmínkám (obr.7.1). Protože však v systému existují integrály pohybu (např. celková energie, případně další integrály - hybnost, různé momenty apod.), lze během výpočtu neustále ověřovat jejich zachování, neboť na jiných trajektoriích budou mít integrály pohybu patrně jinou hodnotu.