9 Simulace konzervativního systému
metoda prediktor-korektor
hraniční křivka pohybu
počáteční podmínky v roli parametrů
pohyb na invariantním toru
zamykání fáze
Poincarého mapa
jednoduché a násobné tory
rozpad toru a chaotická trajektorie
9.1 Definice a
simulace systému se dvěma stupni volnosti
9.2 Konstrukce Poincarého mapy
9.3 Bifurkační diagram konzervativního systému
Disipativní systémy jsou intenzivněji studovány než systémy konzervativní zřejmě také proto, že se vyskytují častěji. Konzervativní systémy mají některé speciální vlastnosti, které lze demonstrovat na jednoduchém případě. Uvažujme modifikovaný rotátor bez tlumení, jehož závěs tvoří nehmotná pružina (viz obr.9.1).
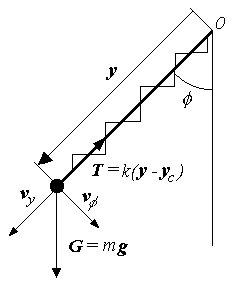
Obr.9.1
Rotátor s pružným závěsem. Na hmotný bod působí kromě gravitace tah
pružného závěsu T. Okamžitou rychlost lze rozložit na dvě složky vy
ve směru pružného závěsu a vf
= ![]() y
ve směru rotačního pohybu, které jsou na sebe zřejmě kolmé.
y
ve směru rotačního pohybu, které jsou na sebe zřejmě kolmé.
Stavové proměnné systému lze přímočaře zvolit např takto:
Parametry systému tvoří
Kinetická energie uvedeného systému je pak dána vztahem
| (9.1) |
Pro potenciální energii platí
| (9.2) |
9.1 Definice a simulace systému se dvěma stupni volnosti
Přejdeme nyní k novým stavovým proměnným, kterými budou zobecněné souřadnice f , y a zobecněné hybnosti pf ,py , které stanovíme ze vztahů
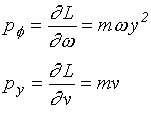 |
(9.3) |
kde L = Ek - Ep je Lagrangeova funkce soustavy. Hamiltonovu funkci lze nyní psát ve tvaru
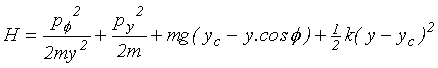 |
(9.4) |
Z Hamiltonových rovnic pak dostaneme soustavu dynamického systému
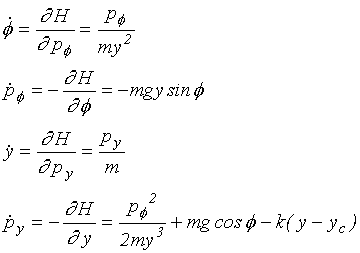 |
(9.5) |
Systém je evidentně nelineární, jeho trajektorie musíme uvažovat ve čtyřrozměrném fázovém prostoru. Z existence integrálu pohybu (celkové energie) je však zřejmé, že trajektorie systému bude ležet na nadploše dané vztahem
| (9.6) |
Nebudeme se pokoušet systém převést na normalizovaný tvar ani hledat další integrály pohybu (systém obecně není integrabilní) a pokusíme se o přímou simulaci systému v definičním tvaru (9.5).
Deklaraci objektu rotátoru musíme rozšířit o nové stavové proměnné a parametry systému. Při simulaci pohybu stejnými metodami jako v kap.8 rychle zjistíme, že metoda Runge-Kutta je velmi neefektivní, systém i při velmi jemném kroku rychle získává energii. Uvedený problém souvisí s velkou aplitudou obou složek energie, které značně převyšují celkovou energii systému (obr.9.2). Ukazuje se, že toto je obecný problém simulace nelineárních konzervativních systémů, který způsobuje malou přesnost výpočtů např. úloh nebeské mechaniky. Mnohem lepší výsledky než metoda Runge-Kutta dávají kombinace Adamsových metod známých pod názvem prediktor-korektor (viz kap.7). Při použití algoritmu PECE 5. řádu jsou již výsledky simulace v dobré shodě se zákonem zachování energie po relativně dlouhou dobu výpočtu.
Pokusíme se dále zobrazit pomocí uvedeného algoritmu prostou trajektorii hmotného bodu v reálné rovině, což je projekce čtyřrozměrné trajektorie do roviny (x1,x2) ş (y cosf ,y sinf ). Podle čl.5.3 je užitečné zároveň zobrazit hraniční křivku potenciální energie, kdy zobecněné hybnosti jsou nulové. Získaná trajektorie by se měla této hranice dotýkat v několika bodech, pokud nemá rotátor nenulovou střední kinetickou energii (tj. rotuje bez bodů vratu). Pro hraniční křivku platí:
| (9.7) |
odkud
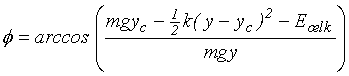 |
(9.8) |
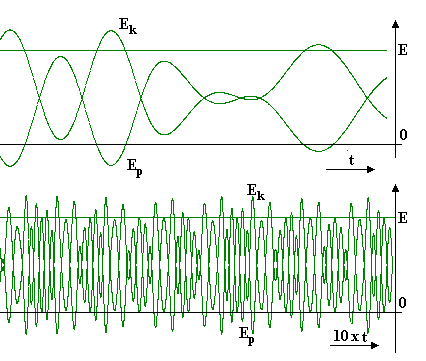
Obr.9.2
Pro zobrazení průběhu energií konzervativního systému (9.5) použijeme metodu
showE() prakticky bez úprav. Pro názornost jsou zobrazeny dvě časové škály.
Hraniční křivka f (y) nemá samozřejmě libovolný definiční obor. Absolutní velikost výrazu uvedeného v závorce vztahu (9.8) musí být menší nebo rovna 1. Při implementaci metody boundary(), která hraniční křivku zobrazí musíme ostatní hodnoty vyloučit. Zároveň lze využít symetrii křivky vzhledem k ose y.
Hlavní program musíme modifikovat zejména z hlediska stanovení počátečních podmínek. Z kap.5 je zřejmé, že v případě konzervativních systémů mají počáteční podmínky podobný význam jako parametry systému, tj. musíme vytvořit možnost stanovení různých počátečních podmínek tak, aby energie systému zůstala stejná. V našem případě budeme tedy definovat počáteční hodnoty zobecněných souřadnic, celkovou energii systému, jednu zobecněnou hybnost zafixujeme a druhou vypočítáme ze vztahu (9.4) tak, aby doplnila energii systému na požadovanou hodnotu.
Průběh reálné trajektorie pro některé hodnoty celkové energie je na obr.9.3-4. Z hraniční křivky vidíme, že systém je nelineární, z obálky trajektorií je zřejmá rovněž neintegrabilita systému. S rostoucí energií systému roste i “nelineárnost” jeho chování.
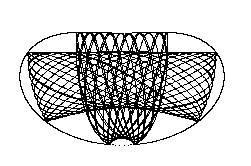
Obr.9.3
Trajektorie koncového bodu pružného rotátoru s celkovou energií E=2 a
počátečními hodnotami zobecněných souřadnic q1=0.1, q2=2 a q1=0.7,
q2=2. Parametry systému jsou: yc= m=1, k=10
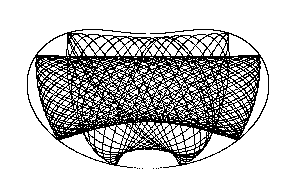
Obr.9.4
Trajektorie koncového bodu pružného rotátoru s celkovou energií E=5. Parametry systému jsou stejné jako na obr.9.3.
Zobrazené trajektorie zachovávají symetrii systému a vyplňují hustě jednoduchou souvislou plochu reálné roviny. Dále uvidíme, že odpovídají kvaziperiodickému pohybu na invariantním toru. Že chování systému v zobrazeném rozmezí není všude triviální, je patrné z obr.9.5. Trajektorie koncového bodu má složitější průběh, dochází k tzv. zamčení fáze, tj. omezení pohybu na podmnožinu očekávané oblasti, kterou by trajektorie měla vyplnit. Nejedná se o případ speciálního periodického pohybu při jedinečném výběru počátečních podmínek, podobné chování s jinou symetrií dostaneme pro široký interval počátečních podmínek.
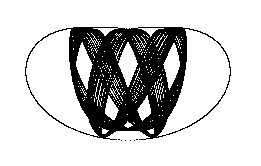
Obr.9.5
Trajektorie koncového bodu pružného rotátoru s energií E=2 a s výběrem počátečních podmínek q1=0.2, q2=2 (srv. s obr.9.3).
9.2 Konstrukce Poincarého mapy
Při podrobnější analýze zjistíme, že chování uvedeného systému pružného rotátoru může být velmi pestré podle celkové energie systému a počátečních podmínek. Omezíme se proto pouze na dvě varianty celkové energie systému podle obr.9.3-4. V obou případech nemá rotátor dostatek energie k tomu, aby vykonánal rotační pohyb kolem osy závěsu. K podrobnější analýze nám již nepostačí reálný pohyb systému a přejdeme proto k efektivnějšímu nástroji v podobě Poincarého map.
Poincarého mapu zkonstruujeme jako řez 4-rozměrným fázovým prostorem pomocí podmínky
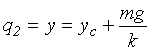 |
(9.9) |
tj. zaznamenáme pouze průchod při rovnovážné délce kyvadla. Navíc se omezíme na kladný směr rychlosti ve směru závěsu, abychom vyloučili protilehlý řez invariantním torem.
Nyní můžeme zobrazit Poincarého mapy odpovídající trajektoriím na obr.9.3-5.
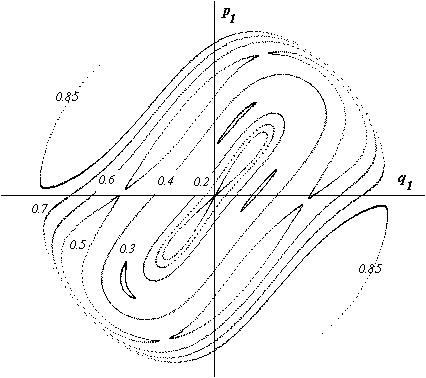
Obr.9.6
Poincarého mapy různých trajektorií pro systém s energií E=2.
Jednotlivé mapy jsou popsány počáteční hodnotou souřadnice q1 (q2=2). Počáteční hodnota nejvnitřnější trajektorie je q1=10-6, tj. prakticky nulový počáteční úhel. Potenciální energie pružiny se však rychle přesune i na gravitační potenciální energii vyvolanou rotačním pohybem (rotátor začne kromě kmitavého pohybu vykonávat i rotační pohyb).
Z obrázku je patrné, že pro tuto hodnotu energie a parametrů systému je jeho pohyb vždy uspořádaný, avšak pro různé počáteční podmínky se střídají oblasti s různým chováním. Mezi trajektoriemi ležícími na jednoduchém toru se objevují oblasti trajektorií na dvoj-, troj- a čtyřnásobném toru, které odpovídají zamčení fáze podle obr.9.5. Poincarého mapy trajektorií v rámci jednotlivých oblastí jsou kvalitativně ekvivalentní, avšak oblasti navzájem ekvivalentní nejsou.
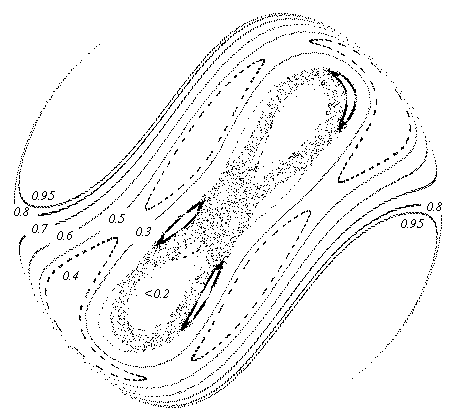
Obr.9.7
Poincarého mapy různých trajektorií pro systém s energií E=5.
Jednotlivé mapy jsou opět popsány počáteční hodnotou souřadnice q1 (q2=2). Vnitřní trajektorie jsou pro počáteční hodnotu q1<0.2 zdánlivě totožné, jedná se o oblast s chaotickým chováním.
Na obrázku 9.7 se opět střídají oblasti s různým druhem pohybu. Nejmarkantnější je však přítomnost chaotické trajektorie v okolí počátku. Její mapa již neleží na souvislé křivce (resp. na soustavě křivek), avšak zaujímá oblast se složitou vnitřní strukturou. Prokázat fraktálový charakter chaotické oblasti je obtížné, neboť trajektorie nemá přitahující charakter (u konzervativních systému se atraktory nevyskytují) a chyba výpočtu rychle roste. Vidíme, že chaotická oblast vznikla interakcí několika druhů chování: obsahuje fragmenty jednoduchého, dvojitého i trojitého toru. Podle úvah z kap.5 je pravděpodobné, že došlo jak k homoklinickému, tak heteroklinickému průniku stabilních a nestabilních variet a pohyb na toru se rozpadl. Zvýrazněná hustota bodů v některých oblastech chaotické mapy napovídá, že některé druhy chování i v chaotickém pohybu převažují, avšak podrobná analýza takových jevů leží mimo rámec tohoto textu.
9.3 Bifurkační diagram konzervativního systému
Poincarého mapy uvedeného typu, tj. s různými počátečními podmínkami vyhovujícími konstantní hodnotě integrálu pohybu, naznačují moožnost vytvoření obdoby bifurkačního diagramu, kde na místě parametu systému figuruje počáteční hodnota vhodně zvolené stavové proměnné. V bifurkačním diagramu však musíme snížit dimenzi původně plošné Poincarého mapy na soustavu intervalů. Nejvhodnější a nejnázornější by patrně bylo provést ještě jednou řez tentokrát Poincarého mapou, např. pomocí podmínky q1=0, a výsledné množiny bodů vynést v závislosti na počáteční hodnotě q10. Pohyb na jednoduchém toru by se takto mapoval do dvou bodů, na zdvojeném toru do jiného počtu bodů atd. Bohužel, tato metoda je výpočetně příliš náročná, neboť pravděpodobnost bodů v Poincarého mapě, které vyhovují podmínce q1=0 je prakticky nulová. Nabízí se možnost rozšíření uvedené podmínky na určitý interval, avšak počet bodů v původní mapě, které by vyhověli malému intervalu bude příliš nízký na vyniknutí tvaru bifurkačního diagramu, pokud nemáme k dispozici výpočetní výkon velkých počítačů. Proto použijeme jednodušší možnost snížení dimenze půvední mapy pouhou projekcí všech bodů do osy p1. Postupovat budeme tedy tak, že pro každou hodnotu q10 vyneseme n souřadnic p1 bodů Poincarého mapy podle obr.9.6-7.
Na obr.9.8 je uvedená obdoba bifurkačního diagramu pro energii systému E=5. Výpočet je časově zdlouhavý, přestože je počet zobrazených bodů pro každou hodnotu počáteční podmínky nízký (100). V diagramu tohoto typu lze ztěží odlišit oblasti kvaziperiodického chování od chaotických oblastí, neboť projekcí se ztratí informace o rozložení bodů v původní mapě. Je však dobře patrný rozpad jednoduchého toru na násobné tory.
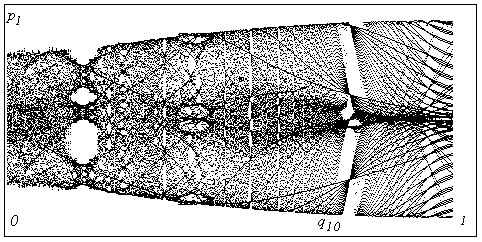
Obr.9.8
Obdoba bifurkačního diagramu pro konzervativní dynamický systém se dvěma stupni volnosti. Body na ose p1 jsou projekcí “plošné” Poincarého mapy. V roli parametru systému vystupují počáteční podmínky splňující požadavek konstantní energie.
Z uvedených poznatků lze učinit několik závěrů o sledovaném systému:
Podrobná a seriózní analýza uvedeného jednoduchého systému přesahuje rámec těchto textů. Je však zřejmá nesmírná pestrost chování systému a potíže, které vyvstanou při pokusu komplexně toto chování popsat. I při opakovaných projekcích a fixaci parametrů systému jsou zobrazené diagramy značně složité a nepřehledné, skutečné komplikace by však nastaly při pokusu zmapovat současné změny počátečních podmínek a parametrů systému.