8   Simulace nelineárního dynamického systému - pokračování

podivný atraktor
vrstevnatá struktura limitní množiny
fraktály
soběpodobnost
bazény přitažlivost
difuzní charakter separatrix
závislost limitních stavů na řídících parametrech
strukturální nestabilita
Feigenbaumovo číslo
teorie katastrof

8.6    Poincarého mapy
8.7    Oblasti přitažlivosti
8.8    Bifurkační diagram
8.9    Dimenze fraktálů

8.6    Poincarého mapy

Znázornění trajektorií je zejména v případě chaotického vývoje málo vypovídající. Modifikujme proto náš program pro znázornění Poincarého mapy, kterou vytvoříme jako řez fázového prostoru rovinami q =2kp. Ve skutečnosti bývá mapa Poincarého definována jako průnik fázového prostoru s jednou nadrovinou, avšak vzhledem k periodické vnější síle lze provést stejnou úvahu jako v případě proměnné f: stav ani vývoj systému se nezmění při změně fáze vnější síly o plný úhel.

Zobrazování se nyní chová jako stroboskop: z trajektorie zobrazujeme body ve vybraných pravidelných časových intervalech. Výsledná mapa je pro limitní cykly velmi jednoduchá - skládá se z jednoho nebo více izolovaných bodů, pro kvaziperiodický pohyb ji tvoří množina bodů na omezeném intervalu určité křivky.

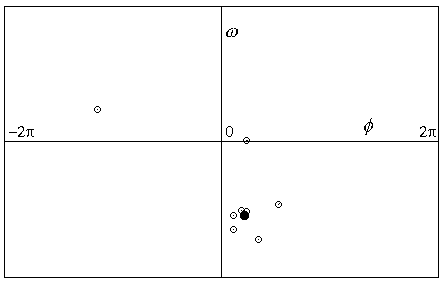
Obr.8.11a

Poincarého mapa pro parametry systému: p=1.06, q=2

Jednotlivé body jsou zvýrazněny, kritický bod odpovídající jednoduchému limitnímu cyklu je vyplněn.
Posloupnost bodů charakterizující ustálení systému do limitního cyklu připomíná okolí stabilního ohniska. Poincarého mapa tak představuje projekci chování systému ve vícerozměrném fázovém prostoru do prostoru nižší dimenze. Limitní cyklus je pak představován jediným kritickým bodem.

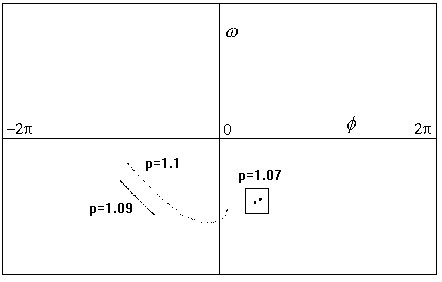
Obr.8.11b

Poincarého mapy pro parametr q=2 v ustáleném stavu:

p=0.7 (zdvojený cyklus),

p=1.09 (kvaziperiodický pohyb)

p=1.1 (mnohonásobně zdvojený cyklus)

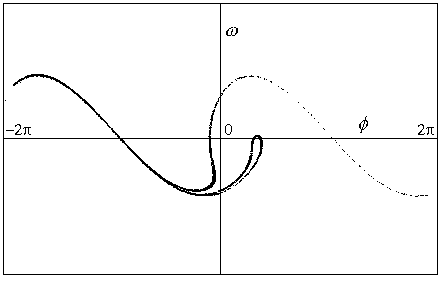
Obr.8.12a

Poincarého mapa pro parametry systému: p=1.15, q=2

Chaotické chování.

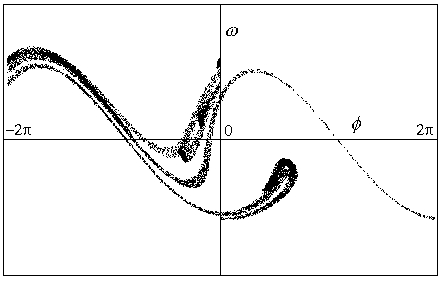
Obr.8.12b

Poincarého mapa pro parametry systému: p=1.5, q=4

Opět chaotický vývoj.
Pro chaotický pohyb však dostáváme složité útvary podle obr.8.12, které představují řez atraktorem. V tomto případě je realizace Poincarého mapy časově náročná: ze všech bodů trajektorie v časovém intervalu D t = 2p/W  realizujeme jenom jeden bod. Pro W = 2/3 a velikost kroku h = 0.01 tak zobrazíme jenom jeden z 1000 vypočtených stavů. Pro vyniknutí tvaru atraktoru musí být však zobrazených bodů velmi mnoho.

Fraktální vlastnosti chaotického chování

Poincarého mapa chaotického pohybu má zajímavé vlastnosti. Nelze předpokládat, že je to mapa jedné skutečné trajektorie. Vzhledem k chybě použité numerické metody a zaokrouhlovací chybě neustále přeskakujeme mezi blízkými trajektoriemi, a tak po dostatečně dlouhé době představují uvedené objekty skutečně řez limitní množinou. Přestože hustota bodů v mapě roste s délkou vývoje systému, nedosáhneme ani při dostatečně přesném výpočtu vyplnění souvislé oblasti. Lze ukázat, že uvedená limitní množina má skutečně složitou vrstevnatou strukturu, která vyplývá z podstaty chaotického pohybu: trajektorie se nemohou protínat, nejsou periodické, původně blízké trajektorie se od sebe rychle vzdalují, avšak přesto je vývoj systému omezen na uzavřenou oblast fázového prostoru. Fázový portrét v ustáleném stavu tvoří tedy trajektorie na "nekonečně zvrásněné" ploše (zjednodušeně si ji můžeme představit jako hladkou plochu, kterou přeložíme přes sebe, výsledek opět přeložíme a tento proces opakujeme bez omezení). Pro tyto vlastnosti byla limitní množina chaotického pohybu nazvána podivný atraktor (strange attractor). Z hlediska teorie míry představuje podivný atraktor nekompaktní množinu s neceločíselnou dimenzí: přesto, že se jedná o plochu (která by měla být dvojrozměrná), její nekonečná vrstevnatost způsobí zvýšení její dimenze na číslo vyšší než 2, avšak nižší než 3 (atraktor nemá objemový charakter). Takové útvary se nazývají fraktály a jednou z jejich charakteristických vlastností je tzv. soběpodobnost. Tím je myšlena "podobnost" dvou úseků fraktálu v různém měřítku. "Podobnost" je zde opět chápána jako existence vzájemně jednoznačného zobrazení jednoho úseku na druhý (viz definici kvalitativní ekvivalence v čl.3.3). Absolutní relativnost měřítka, (tj. libovolně malý detail fraktálu je stejně složitý jako původní úsek), má za následek nekonečně velkou členitost výsledného útvaru. Je zřejmé, že dimenze Poincarého mapy z obr. 8.12 odpovídá dimenzi atraktoru snížené o jednotku.

8.7    Oblasti přitažlivosti

Na obr.8.9k jsou zobrazeny limitní cykly našeho systému pro parametry p=1.30, q=2 a W =2/3. Jeden cyklus odpovídá nepravidelnému otáčení rotátoru ve směru a druhý proti směru hodinových ručiček. Pokud existují dva limitní cykly, musí existovat též oblasti (bazény) přitažlivosti ve fázovém prostoru, které obsahují body, ze kterých systém dospěje do jednoho z obou limitních cyklů. Pro zobrazení takových oblastí již nelze použít fázový portrét podle obr.8.4 (pro vícerozměrný fázový prostor je obvykle fázový portrét zcela nepřehledný). Vytvoříme proto metodu cycle(...), která na základě počátečních podmínek zjistí, do kterého typu limitního cyklu systém zkonvergoval. K rozlišení cyklů použijeme s výhodou fakt, že v cyklu typu A je úhel rotátoru všude kladný a v cyklu B záporný (viz obr.8.9k). Metoda tedy "nechá" systém vyvíjet se dostatečně dlouhou dobu a pak podle znaménka úhlu vrátí logickou hodnotu (0/1).

Nyní vytvoříme metodu, která zmapuje oblast přitažlivosti showBas(...). Její činnost bude jednoduchá: zadanou pravoúhlou oblast fázové roviny (f,w) rozdělí do rastru, z každého pole rastru pak vybere jeden bod a zjistí jeho limitní cyklus. Metoda vyznačí jednou barvou pole rastru, z něhož systém dospěje do cyklu A a jinou barvou pole, z něhož systém dospěje do cyklu B. "Skenování" větší oblasti je opět časově náročné, proto je třeba volit rastr dosti hrubý.

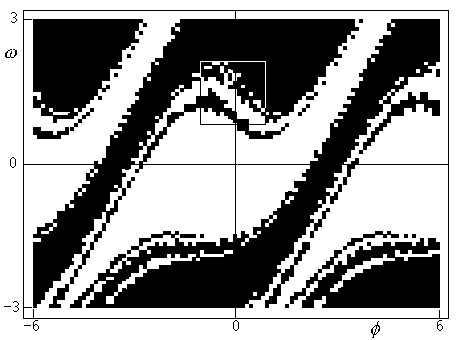
Obr.8.13a
Bazény přitažlivosti limitních cyklů podle obr.8.9k

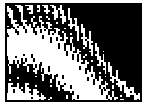
Obr.8.13b
Výsledek podrobnější analýzy vybrané oblasti z obr.8.13a

Na obr.8.13 je odpovídající mapa bazénů přitažlivosti uvedených cyklů. Tvar oblastí přitažlivosti je ve srovnání s neřízeným rotátorem (viz obr.8.4) podstatně složitější. Hranice oblasti (separatrix) má zřetelně difuzní charakter a po zvětšení (zjemnění kroku v metodě showBas) je zřejmé, že separatrix bazénů přitažlivosti v případě, že systém má více limitních cyklů, je fraktál. V okolí některých bodů rozhraní je tedy nemožné odhadnout, kam systém zkonverguje. Proto i naše mapa je pouze ilustrativní a principiálně nikdy nemůže být přesná. Fraktálová členitost rozhraní způsobuje, že existuje množina bodů (s dimenzí vyšší než má množina bodů jednoduchého rozhraní), v nichž se systém chová nestabilně, tj. dvě trajektorie procházející libovolně blízkými body se rychle vzdalují do různých limitních stavů. Když se parametry systému blíží hodnotám umožňujícím chaotický vývoj systému, jsou hranice bazénů přitažlivosti stále rozmazanější. V případě limitního stavu v podobě jediného cizího atraktoru ztrácí pojem oblasti přitažlivosti smysl, limitní stavy splývají. Chaotický atraktor je tedy oblastí nestability systému, což se může zdát vzhledem k jeho přitahující vlastnosti poněkud paradoxní (nestabilita je tradičně spojována s odpuzující vlastností, viz např. odpuzující cyklus - tzv. repellor).

Pokusíme se dále zobrazit bazény přitažlivosti pro takové parametry systému, kdy existuje větší počet limitních cyklů. Z obr. 8.9 plyne, že systém dosahuje pro parametr p=1.08 v našem oboru počátečních podmínek dvou kvalitativně odlišných cyklů. Jeden z nich má navíc dvě symetrické varianty. Metodu cycle(...) musíme poněkud upravit s ohledem na skutečnost, že Poincarého mapa uvedených cyklů sestává z většího množství bodů (došlo ke zdvojení periody). Ke zjištění ustálení systému tedy použijeme více průchodů systému limitním cyklem a konvergenci budeme sledovat na průměru odpovídajících bodů v Poincarého mapě. Stejně tak bude tato průměrná hodnota odlišovat jednotlivé limitní cykly. V metodě showBas(...) pak zobrazíme oblast rastru, z níž systém dospěje do daného limitního cyklu, pro každý cyklus jinou barvou. Výsledek upravené metody showBas(...) je na obr.8.13c. Oblasti přitažlivosti mají zajímavý charakter již jen vzdáleně připomínající původní bazény přitaživosti nebuzeného tlumeného rotátoru na obr.8.4. Periodicky se opakuje zřetelně fraktálový motiv, nestabilní hraniční oblasti jsou značně nepřehledné (srv. s obr.8.13a).

Obr.8.13c

Zobrazení bazénů přitažlivosti v případě existence více typů limitních cyklů Je zřejmě, že díky fraktálové struktuře existuje poměrně velká oblast fázového prostoru, kde nelze určit, do kterého limitního cyklu systém zkonverguje.

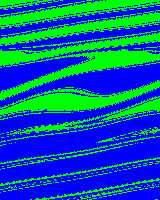
Obr.8.13d  Ilustrace zvětšování difuzní oblasti hranic oblastí přitažlivosti se zvětšující amplitudou vnější síly p (nelinearitou). Použit byl jemnější rastr a větší oblast vyšetřovaná oblast. (Doba výpočtu se může prodloužit i na několik hodin).

Obr.8.13e  Různé typy bazénů přitažlivosti jednoduchých nelineárních disipativních systémů (zdroj: Internet)

8.8    Bifurkační diagram

Předcházející diagramy se týkaly různých metod vizualizace vývoje systému při pevných hodnotách řídících parametrů systému. Dalším důležitým typem diagramu je závislost limitních stavů systému na některém z řídících parametrů. Již víme, že limitní stav systému lze vystihnout efektivně Poincarého mapou, kterou dále promítneme do osy úhlové rychlosti w. Vznikne tak závislost limitní úhlové rychlosti (ve "stroboskopickém" režimu Poincarého mapy) na velikosti aplitudy p harmonické vnější síly. Protože může existovat více hodnot úhlové rychlosti v mapě pro jednu hodnotu parametru p (viz zdvojení periody nebo kvaziperiodický pohyb), bude výsledná závislost víceznačná. K vytvoření diagramu použijeme metodu showBif(...), která pro daný rozsah hodnot parametru p zobrazí odpovídající hodnoty limitní úhlové rychlosti. Metoda pracuje následovně: pro každou hodnotu parametru p nechá systém ustálit, a dále zobrazí 50 hodnot proměnné w ve stavech, kdy q =2kp. Pokud bude limitní cyklus jednoduchý, zobrazí se 50 identických bodů, v případě zdvojených cyklů nebo chaosu se zobrazí prvních 50 hodnot w v mapě Poincarého.

Poznámka: Při implementaci nemůžeme testovat ustálení cyklu podle vzdálenosti posledních bodů v Poincarého mapě (jako v případě metody cycle()), neboť Poincarého mapa nemusí obecně obsahovat pouze jeden limitní bod. Pro ustálení se spokojíme proto s 30 úplnými cykly q , což v našem systému empiricky stačí. Při nové hodnotě parametru p nastavíme vždy znovu počáteční podmínky na náhodné hodnoty, jinak může systém některé limitní stavy vynechat. Ve skutečnosti bychom měli pro každou hodnotu p nalézt všechny limitní stavy, to je však v okolí chaotického chování prakticky nemožné.

Obr.8.14a

Diagram získaný pomocí metody showBif.
Při zvyšující se hodnotě amplitudy p vnější síly se původně jednoduchý cyklus štěpí na zdvojený, kterému odpovídají dvě hodnoty úhlové rychlosti v Poincarého mapě. Toto zdvojování se v různých variantách opakuje. Zdvojený limitní cyklus není kvalitativně ekvivalentní s jednoduchým cyklem, proto v oblasti štěpení dochází ke strukturální nestabilitě systému: malá změna hodnoty řídícího parametru způsobí kvalitativně rozdílné chování systému. Kromě zdvojování cyklů dochází také k bifurkaci prostřednictvím vzniku dalších možných limitních stavů. Diagram na obr.8.14a se nazývá bifurkační diagram. Z obrázku jsou patrné oblasti limitních cyklů střídaných oblastmi kvaziperiodického pohybu a chaosu. Dá se opět ukázat, že diagram má fraktálový charakter, tj, při dostatečně jemné změně řídícího parametru i ve zdánlivě souvislé chaotické oblasti opět nalezneme oblasti bifurkujících cyklů.

Na obr.8.14b je analogický diagram avšak se spojitým vývojem dynamického systému, kdy nenastavujeme náhodné počáteční podmínky při každé změně parametru p. Vidíme, že systém se může některým oblastem stavů úplně vyhnout a tyto limitní stavy se pak v bifurkačním diagramu vůbec neobjeví. Bifurkace jsou pak patrné pouze změnou průběhu úhlové rychlosti w(p), kde vzniká skok v první derivaci. Dále se systém může vyvíjet podél jedné bifurkační větve. Zda se v takovém diagramu zobrazí více stavů, závisí na tvaru oblastí přitažlivosti. Vyšetřováním výskytu bifurkací v závislosti na změně parametrů se zabývá tzv. teorie katastrof.

Obr.8.14b

Bifurkační diagram při stejných podmínkách jako na obr.8.14b, avšak systém se vyvíjí spojitě při současné změně řídícího parametru.

Pokud došlo pro hodnotu parametru p_i k bifurkaci, pro hodnotu p_i+1 k další bifurkaci atd., platí zajímavý generický vztah:

kde d je univerzální konstanta za určitých podmínek nezávislá na tvaru funkce F reprezentující dynamický systém (tzv. Feigenbaumovo číslo).

Poznámka:
V čl.4.1 bylo ukázáno, že Poincarého mapu lze chápat jako zobrazení, které přiřazuje bodu ve fázovém prostoru nový průchod trajektorie Poincarého rovinou. Naše simulované dynamické systémy nemají analyticky vyjádřitelnou Poicarého mapu. Jednoduché analytické mapy však lze vytvářet a studovat jejich vlastnosti. Ukazuje se, že nelineární vztahy v definici takových map vedou k obdobě složitého chování, které jsme viděli při simulaci spojitých systémů. Patrně nejznámější je tzv. logistická mapa, která přiřazuje bodu na přímce nový bod jednoduchým kvadratickým vztahem. Kvadratická nelinearita způsobuje výskyt jak násobných bodů (analogie zdvojování periody), tak chaotické chování. Změnou koeficientu (parametrem) u nelineárního členu lze dosáhnout různé druhy vývoje a získat také obdobu bifurkačního diagramu. Všechny iterační výpočty jsou zcela triviální, a tak lze studovat i velmi jemné vlastnosti, které jsou u spojitých systémů velmi obtížně pozorovatelné. Podrobný bifurkační diagram logistické mapy je na tomto obrázku (je značně velký).

8.9    Dimenze fraktálů

Již bylo řečeno, že fraktály jsou množiny, jejichž dimenze je neceločíselná. Pro zjištění velikosti dimenze bylo zavedeno několik zobecněných definic dimenze, které jsou detailněji studovány v teorii míry. Jednou z jednodušších definic je Kolmogorovova dimenze (kapacita) d_c:

Uvažujme úsečku délky L, kterou pokryjeme N stejně dlouhými intervaly délky e. Minimální počet intervalů N(e), které pokrývají celou úsečku je závislý na délce intervalů podle vztahu:

Pokud budeme měřit délku křivky, můžeme postupovat obdobně a vyjádřit délku křivky vztahem

Stejně tak lze pokrýt plochu čtverce o straně L počtem N(e) čtverců o straně e, přičemž pro plochu čtverce platí:

Pro obecný rovinný útvar o ploše L₂ pak lze psát:

Obecně pro d-rozměrný útvar dostáváme:

odkud plyne možnost vyjádřit dimenzi d množiny o "objemu" L_d takto:

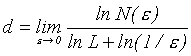
Pokud bude "objem" množiny konečný, plyne z uvedeného vztahu definice Kolmogorovovy dimenze, který již na objemu množiny nezávisí:

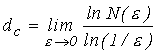
Takto definovaná dimenze odpovídá přirozeným představám o dimenzi prostorových útvarů a hodí se pro vyčíslení dimenze fraktálových množin.

Známá je tzv. Cantorova fraktálová množina v R definovaná následovně:

Vezměme uzavřený jednotkový interval, rozdělme ho na třetiny a prostřední interval z množiny vyjmeme. Na oba zbylé krajní intervaly aplikujeme stejné pravidlo a tímto způsobem pokračujeme bez omezení. Dimenzi Cantorovy množiny v Kolmogorovově pojetí lze vyjádřit z následující posloupnosti:
pro první dělení původního intevalu potřebujeme na pokrytí N(e)=1.(1/e) intervalů, což pro délky intervalů e=1/3 dává N(1/3)=2. Při dalším odstranění středů zbylých krajních intervalů dostaneme obdobně pro délku intervalů e = 1/9 počet N(1/9)=4. Po i-tém dělení pak zřejmě platí:

N (1/3ⁱ) = 2ⁱ

což v limitním přechodu dává pro dimenzi Cantorovy množiny:

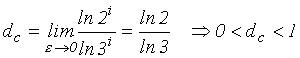
Dimenze uvedené množiny tedy neodpovídá ani množině izolovaných bodů (d=0) ani množině odpovídající intervalu v R (d=1).

Experimentálně zjištěná dimenze Poincarého mapy cizího atraktoru našeho systému je . Při jejím stanovení lze skutečně postupovat tak, že se konstruuje graf ln(N)- ln(1/e) a dimenze se stanovuje extrapolací směrnice grafu pro .