6    Strukturální nestabilita a bifurkace

bifurkační body
strukturální nestabilita
generické vlastnosti systému
bifurkace sedlo-uzel
Hopfova bifurkace

6.1    Bifurkace sedlo-uzel
6.2    Hopfova bifurkace

V předcházející kapitole byla analyzována kvalitativní změna chování systému při změně parametru. V odst.3.3 bylo naznačeno, že úplná analýza dynamického systému spočívá v nalezení kvalitativních vlastností fázových portrétů pro všechny možné hodnoty parametrů systému a výsledek takové analýzy pro lineární rovinné systémy reprezentuje obr.3.7. I pro jednoduché nelineární systémy je taková vyčerpávající analýza velmi obtížná (spíše však nemožná), a proto se při jejich vyšetřování používají různé strategie. Jednu z nejdůležitějších představuje hledání tzv. bifurkačních bodů. Předpokládejme, že systém má jenom jeden parametr (v případě většího počtu parametrů vybereme jeden a ostatní zafixujeme). Zkoumejme nyní fázové portréty systému při spojité změně parametru. Obvykle jsou pro malé změny parametru kvalitativně ekvivalentní. Kritickou hodnotu parametru, při níž se fázový portrét kvalitativně mění nazýváme bifurkačním bodem. Je zřejmé, že bifurkační body mají klíčový význam, neboť oddělují oblasti (v parametrickém prostoru), v nichž se systém chová kvalitativně stejně. V okolí bifurkačního bodu hovoříme o strukturální nestabilitě systému. Hledat bifurkační body lze podle určitých symptomů, nalezení obecného postupu je však zatím v nedohlednu. Bifurkace, k nimž může docházet, lze klasifikovat a v současné době byla posána řada mechanizmů, které k bifurkaci určitého druhu vedou. Ukazuje se, že bez ohledu na konkrétní dynamický systém existují určité obecné jevy, se kterými se setkáváme ve velmi širokých třídách dynamických systémů. Tyto jevy se nazývají generickými vlastnostmi a druhy bifurkací k nim také patří. Hledání nových generických vlastností dynamických systémů a jejich vysvětlení je předmětem intenzívního výzkumu možná také proto, že řada z nich má zatím dosti záhadný charakter. Obecná teorie bifurkací leží mimo rámec tohoto textu, pro názornost zde však uvedeme příklady nejběžnějších typů bifurkací u rovinných systémů.

Uvažujme rovinný jednoparametrický systém definovaný soustavou

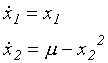(6.1)

s reálným parametrem m.

Hledejme linearizaci systému pro hodnotu parametru m=0. Je zřejmé, že systém má v tomto případě v počátku pevný bod a jeho linearizace je

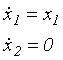(6.2)

Jedna z vlastních hodnot linearizační matice je nulová, systém má tedy v počátku nejednoduchý nehyperbolický pevný bod. Pro hodnotu parametru m <0 systém nemá žádný pevný bod, naopak pro m >0 má systém dva pevné body: jeden sedlový, druhý nestabilní uzel. Celkově je vývoj fázového portrétu patrný z obr.6.1. Bifurkačním bodem je evidentně bod m=0, nové dva pevné body se za tímto bodem od sebe vzdalují úměrně koeficientu ("rychlost" jejich vzdalování vzhledem k parametru m je tedy v okolí bifurkačního bodu nekonečná). Uvedený typ bifurkace se nazývá bifurkace sedlo-uzel a jeho typickou vlastností (symptomem) je vznik dvou pevných bodů a jejich vzdalování při spojité změně parametru (resp. přibližování dvou pevných bodů a jejich zánik při opačném vývoji parametru). U rovinných systémů je výskyt těchto bifurkací podmíněn nulovostí jedné z vlastních hodnot linearizační matice v nehyperbolickém pevném bodě a je generickou vlastností mnoha dynamických systémů.

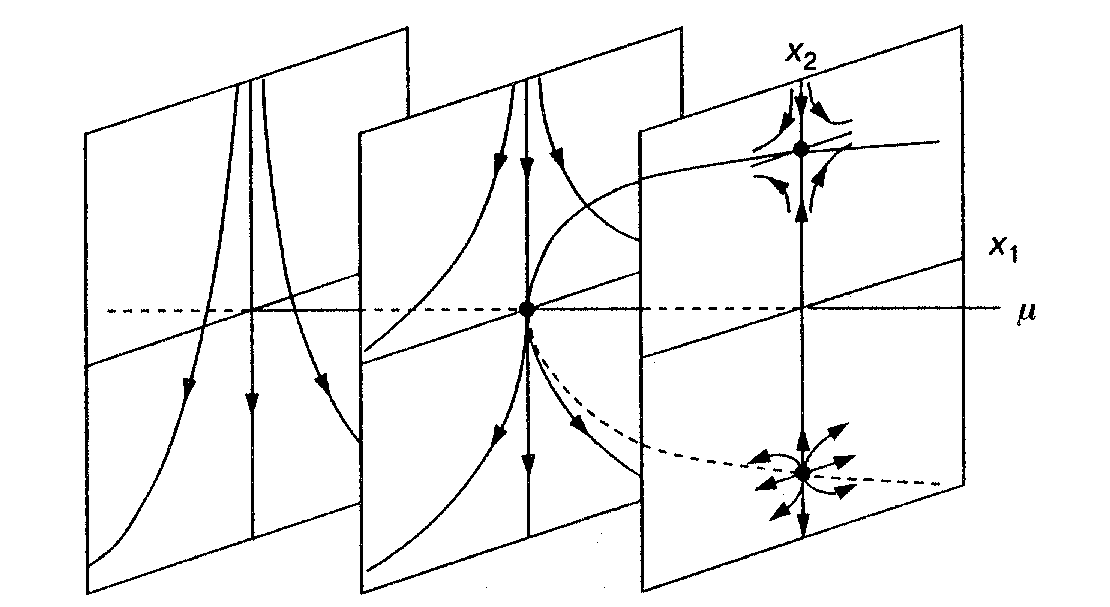
Obr.6.1 Bifurkace sedlo-uzel v rovinném dynamickém systému. Charakteristickým rysem systémů vykazujících tento druh bifurkace je přítomnost kvadratických nelinearit.

Uvažujme nyní dynamický systém definovaný soustavou

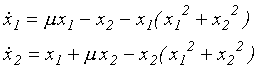(6.3)

Pro hodnotu parametru m=0 má systém pevný bod v počátku a obě vlastní hodnoty linearizační matice jsou ryze imaginární, tj. systém má pro uvedenou hodnotu parametru v počátku jednoduchý nehyperbolický pevný bod. Vztahy (6.3) lze přechodem k polárním souřadnicím vyjádřit v přehledné formě:

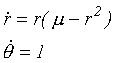(6.4)

Vývoj fázového portrétu pro různé hodnoty parametru je na obr.6.2. Pro záporné hodnoty parametru má fázový portrét v počátku stabilní ohnisko, pro kladné existuje limitní cyklus, jehož poloměr se s rostoucí hodnotou parametru zvětšuje. Bifurkačním bodem je zde opět bod m=0, uvedený typ bifurkace se nazývá po svém objeviteli Hopfův. Nutnou, nikoli však postačující podmínkou tohoto bifurkačního mechanizmu, je u rovinných systémů nehyperbolický pevný bod s ryze imaginárními vlastními hodnotami linearizační matice. Jednorozměrná Poincarého mapa definovaná např. podmínkou x₂=0 má v počátku pevný bod pro záporné hodnoty parametru, pro kladné hodnoty jsou pevné body dva (odpovídají dvěma průnikům limitního cyklu rovinou řezu) a opět se v okolí bifurkačního bodu vzdalují nekonečnou rychlostí. Vidíme, že v okolí bifurkačního bodu se změna chování v obou bifurkačních mechanizmech děje velmi rychle (prakticky skokem).

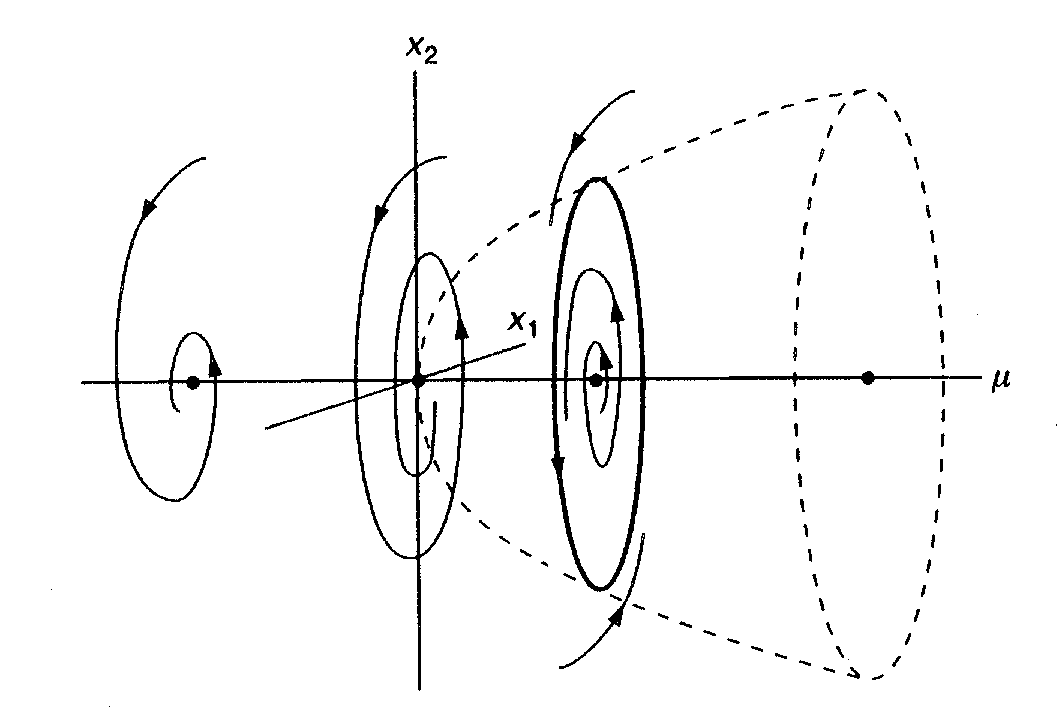
Obr.6.2 Výskyt Hopfovy bifurkace v rovinném jednoparametric-kém systému. V bifurkačním bodě dochází k tzv. zrodu limitního cyklu (resp. k jeho zániku).