4    Nelineární dynamické systémy

okolí bodu fázového prostoru
lokální fázový portrét
linearizace dynamického systému
stabilní a nestabilní pevné body
asymptotická a neutrální stabilita
Ljapunovovův teorém stability
první integrál
konzervativní systém
globální fázový portrét
obyčejné body fázového portrétu
limitní body, limitní množiny a limitní cykly
oblasti záchytu a bazény přitažlivosti
stabilní a nestabilní variety

Pevný bod fázového portrétu obecného systému popsaného vztahem (2.1) se vyznačuje nulovým tokem, proto musí rychlost toku v pevném bodě vyhovovat vztahu:

(4.1)

Protože se trajektorie dynamického systému ve fázovém prostoru nemohou nikde protínat, je zřejmé, že pevné body jsou rozhodující pro kvalitativní popis fázového portrétu. Jediný kritický bod určující typ jednoduchého lineárního systému může být v případě nelineárních systémů nahrazen více kritickými body s různým charakterem. Přesto lze použít základní klasifikaci uvedenou v kap.3 (stabilní, nestabilní uzel, ohnisko, střed apod.). Navíc však vzniká mnoho nových jevů, které nemají přímou analogii v lineárních systémech. Nezbytné definice a věty uvedeme kvůli jednoduchosti a názornosti nejprve pro dynamické systémy omezené na rovinu (se dvěma stavovými proměnnými).

Poznámka:
Důkazy většiny tvrzení nebudeme kvůli přehlednosti uvádět (problematika nelineárních dynamických systémů je příliš rozsáhlá, a proto jsou zde uvedeny jenom fundamentální definice a některé jednodušší závěry).

Okolím o poloměru r bodu fázového prostoru x₀ nazýváme množinu bodů definovanou vztahem { x: |x - x₀ | < r } (okolí je tedy n-rozměrná koule). Lokální fázový portrét je pak fázový portrét v podmnožině fázového prostoru definované jako okolí stanoveného bodu. Fázový portrét jednoduchého lineárního systému je kvalitativně ekvivalentní s lokálním fázovým portrétem v libovolném okolí pevného bodu. Základní myšlenkou vyšetřování nelineárních systémů pak je hledání takového okolí jejich pevných bodů, v němž je jejich lokální fázový portrét kvalitativně ekvivalentní s některým typem lineárního systému (viz obr.4.1).

Obr.4.1 Příklad fázového portrétu nelineárního systému s nestabilním a sedlovým kritickým bodem a stabilním ohniskem.

Omezme se nejdříve na základní terminologii dvourozměrných nelineárních systémů (rovinných)

Linearizovaný systém

Uvažujme nelineární dynamický systém v rovině, který je popsán soustavou:

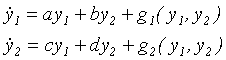(4.2)

kde nelineární vektorová funkce g má následující vlastnost:

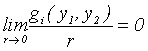(4.3)

r je poloměr okolí kritického bodu v počátku.

Soustavu

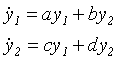(4.4)

pak nazýváme linearizací dynamického systému.

Příklad 4.1

Hledejme linearizaci nelineárního systému daného soustavou

Kritické body vyhovují soustavě rovnic

Bod (-1,1) je jediným řešením uvedené soustavy, systém má tedy jediný pevný bod. Abychom nalezli linearizaci v jeho okolí, musíme transformovat proměnné tak, aby kritický bod ležel v počátku fázového prostoru:

Po dosazení a rozvinutí exponenciální funkce dostaneme hledanou linearizaci:

Linearizace dynamických systémů je důležitou metodou vyšetřování jejich chování. Charakter kritických bodů lze stanovit na základě mnoha užitečných vět, které byly na tomto poli zformulovány, zde uvedeme jenom některé základní pojmy a teze, které využijeme v příkladech simulovaných dynamických systémů v následujících kapitolách.

Pomocí Taylorova rozvoje dynamického systému v okolí pevného bodu (x₁₀ , x₂₀) lze snadno ukázat, že pro koeficienty matice A linearizovaného systému platí:

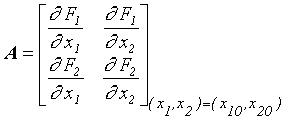(4.5)

Linearizační teorém

Pokud je v okolí jednoduchého kritického bodu nelineárního dynamického systému fázový portrét kvalitativně ekvivalentní s jeho linearizací, pak uvedený kritický bod není středem.

Poznámka:
Kritický bod je jednoduchý, pokud odpovídající linearizovaný systém v tomto bodě je jednoduchý.

Uvedený teorém je platný pouze pro dynamické systémy v rovině. Středový pevný bod je podle něj jedinou výjimkou, kdy fázový portrét nelineárního systému není v okolí tohoto bodu kvalitativně ekvivalentní s jeho (jednoduchou) linearizací. Přirozeným způsobem lze pak definovat hyperbolické pevné body nelineárních systémů jako body, v jejichž okolí je odpovídající linearizovaný systém hyperbolický. Podle vztahu (4.5) je zřejmé, že hyperbolické pevné body se vyznačují nenulovou reálnou složkou všech vlastních hodnot linearizační matice.

Linearizace v nejednoduchém bodě však neposkytuje informace o chování nelineárního systému (to je zřejmé již z faktu, že linearizovaný fázový portrét obsahuje množinu pevných bodů) (viz obr.4.2)

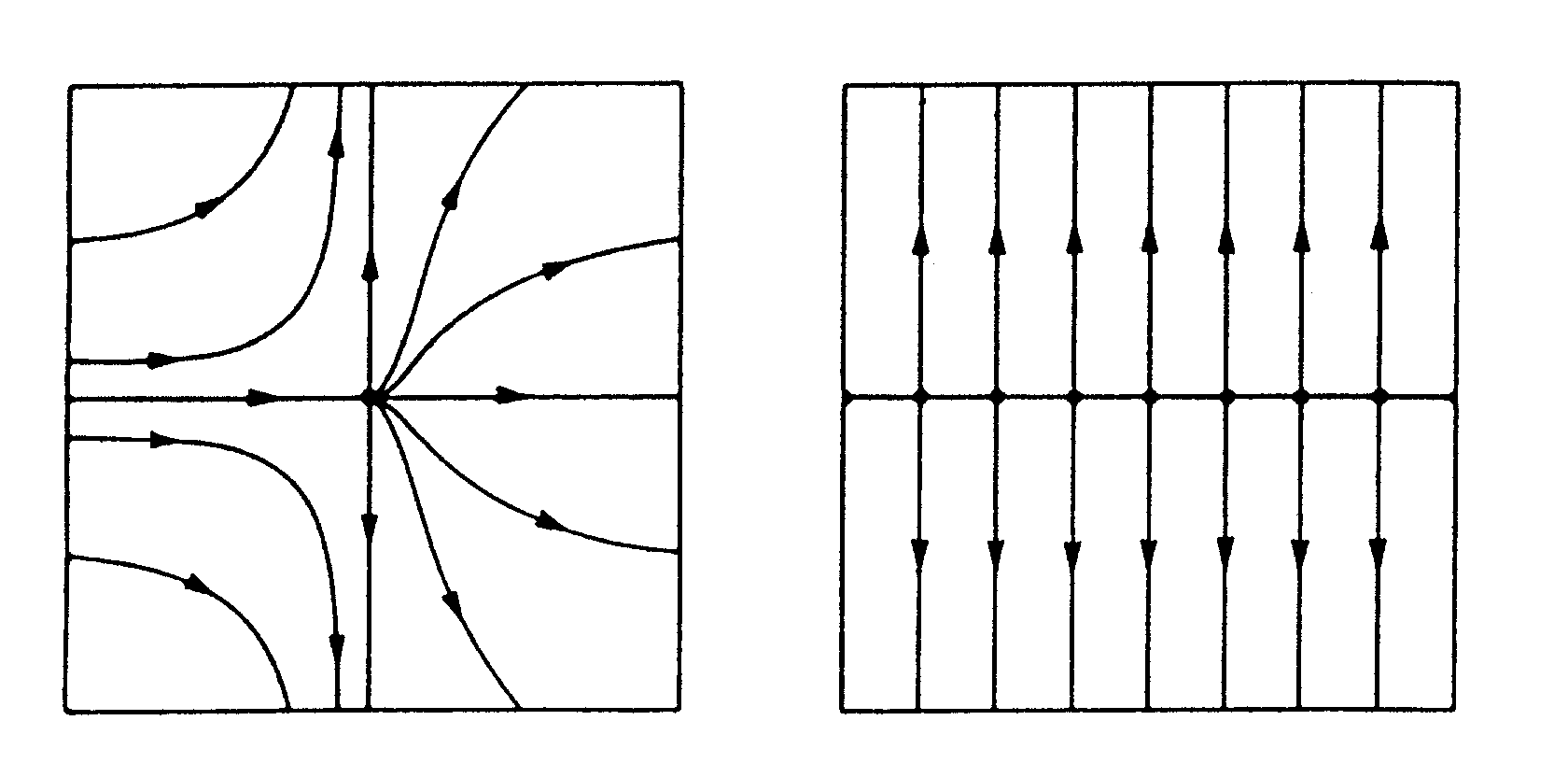
Obr.4.2 Srovnání fázových portrétů nelineárního systému:

a jeho linearizace v okolí kritického bodu (0,0):
kde osa x₁ tvoří množinu pevných bodů.

V současnosti neexistuje ucelený klasifikační systém nejednoduchých pevných bodů založený na klasifikaci jednoduchých bodů lineárních systémů. Je to zřejmě dáno tím, že mnoho kvalitativně odlišných systémů může mít v nejednoduchém pevném bodě stejnou linearizaci. Určité vodítko však poskytují kritéria stablity pevných bodů:

Stabilita kritického bodu

Kritický bod nazýváme stabilním, jestliže ke každému okolí N tohoto bodu existuje okolí takové, že všechny trajektorie, které ním procházejí, zůstávají v okolí N při rostoucím času. Kritický bod, který není stabilní se nazývá nestabilní.

Kritický bod se nazývá asymptoticky stabilní, pokud je stabilní a existuje jeho okolí takové, že každá trajektorie procházející tímto okolím se blíží k uvedenému kritickému bodu při rostoucím času.

Stabilní bod, který není asymptoticky stabilní se nazývá neutrálně stabilní.

Poznámka:
Typickým neutrálně stabilním bodem je středový bod. Uzavřené trajektorie se z jeho okolí nevzdalují, ale do středu rovněž nesměřují.

Ljapunovův teorém stability

Jestliže na nějakém okolí kritického bodu existuje zobrazení V fázového prostoru do R takové, že:

1. gradient 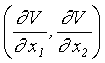existuje a je spojitý

2. V je positivně definitní

3. je negativně definitní

pak je kritický bod asymptoticky stabilní.

Zobrazení V se nazývá Ljapunovova funkce.

Poznámka:
Zobrazení je positivně (negativně) definitní na množině N, jestliže pro každé platí: V(x)>0 (V(x)<0)

Pro rovinné systémy není důkaz Ljapunovova teorému obtížný. Bod 3 teorému vyjadřuje derivaci Ljapunovovy funkce ve směru trajektorie systému. Je zřejmé, že v mnoha systémech může hrát roli Ljapunovovy funkce skalární potenciál.

První integrál

Spojitě diferencovatelná funkce se nazývá prvním integrálem dynamického systému, pokud platí f(x(t))=konst. pro každou trajektorii systému.

Dynamický systém, pro jehož všechny trajektorie existuje první integrál, se nazývá konzervativní.

Poznámka:
V problémech mechaniky může být zřejmě prvním integrálem Hamiltonián a konzervativnost vyjadřuje např. zákon zachování energie.

Globální fázový portrét

Body fázového portrétu, v nichž neplatí (4.1) se nazývají obyčejné. Ke každému obyčejnému bodu existuje okolí neobsahující pevný bod. Všechna tato okolí jsou kvalitativně ekvivalentní. Z uvedeného však neplyne, že globální fázový portrét je zcela určen lokálními fázovými portréty v okolí pevných bodů systému.

Příklad 4.2

Uvažujme systém

Systém je nelineární a má dva jednoduché pevné body (0,0) a (2,0) (již víme, že lineární systém může mít pouze jeden jednoduchý pevný bod). V prvním bodě je linearizace:

V druhém pevném bodě je linearizace systému:

Podle kap.3 jsou oba body v linearizovaném okolí sedlového typu. Oba pevné body jsou navíc hyperbolické, linearizace jsou tedy kvalitativně ekvivalentní s lokálními fázovými portréty původního systému. Přesto existují dva globální fázové portréty vyhovující zjištěnému charakteru pevných bodů (viz obr. 4.3)

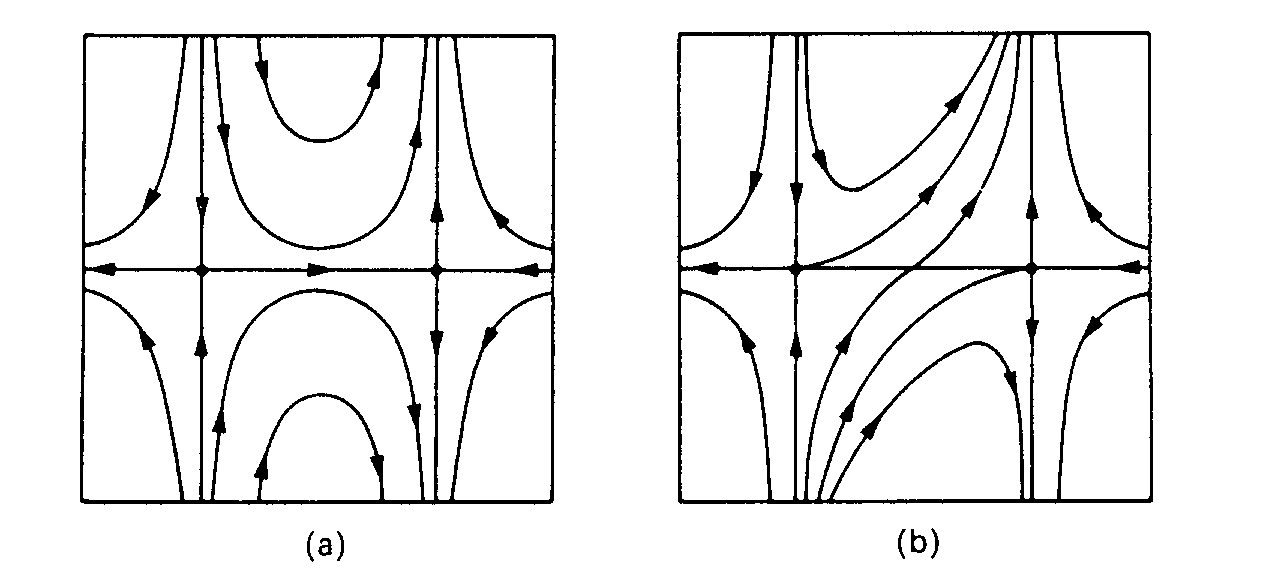
Obr.4.3 Neekvivalentní globální fázové portréty s ekvivalentní linearizecí v pevných bodech. V prvním případě jsou pevné body spojeny trajektorií a neexistuje bijektivní zobrazení jednoho portrétu na druhý. Správně popisuje původní dynamický systém fázový portrét (a).

Limitní body

Limitním bodem y bodu x ve fázovém prostoru nazýváme bod, k němuž se blíží trajektorie
procházející bodem x pro , tj.

Bod y se nazývá též w-limitním (trajektorie do něj směřuje), přičemž a-limitní bod je definován obdobně, avšak trajektorie  z tohoto bodu vychází ().

Limitní množina a limitní cyklus

U nelineárních systémů nemusí trajektorie nabývat pouze jedné hodnoty pro . Množina bodů, kterými trajektorie pro prochází, se nazývá limitní množina a bývá označována Lw(x), resp. La(x).

Pokud je limitní množinou uzavřená křivka (orbit), nazývá se limitní cyklus.

Poznámka:
Limitní cyklus je poměrně důležitá vlastnost nelineárních systémů, jak dále uvidíme. Systém může dosáhnout limitní cyklus, v němž pak setrvá, po pestrém a dlouhém vývoji.

Poincaré-Bendixsonův teorém

Pokud je limitní množina kompaktní a neobsahuje limitní bod, tvoří ji uzavřená křivka (orbit).

Poznámka:
Systém se tedy po dostatečně dlouhém vývoji stabilizuje do konstantního stavu nebo periodického pohybu. U chaotických systémů uvidíme, že tomu tak není, neboť jejich limitní množina není kompaktní.

Oblast záchytu

Množina bodů ve fázovém prostoru taková, že všechny trajektorie procházející body této množiny v čase t=0 zůstávají pro t>0 v této množině, se nazývá oblast záchytu. Pokud navíc v oblasti záchytu existuje neprázdná limitní množina, nazývá se oblast záchytu často bazén přitažlivosti. Lze ukázat, že neobsahuje-li oblast záchytu pevný bod, pak existuje v této oblasti limitní cyklus.

Nerovinné nelineární dynamické systémy

Při přechodu k systémům s větším počtem stavových proměnných lze některé definice zavedené u rovinných systémů přirozeným způsobem zobecnit. Často však neexistuje pro takové zobecnění přímá cesta a původně jednoduché pojmy a věty mají pro vícerozměrné systémy poměrně komplikovaný charakter.

Linearizovaný fázový portrét v pevném bodě můžeme definovat pomocí (4.5). Matice linearizovaného systému je dána vztahem:

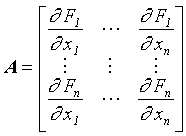(4.6)

kde všechny derivace jsou v pevném bodě systému. Mají-li všechny vlastní hodnoty matice nenulovou reálnou složku, nazýváme odpovídající pevný bod hyperbolickým.

Separatrix linearizovaného systému tvoří podle kap.3 stabilní a nestabilní vlastní prostory, jejichž dimenze závisí na počtu kladných a záporných reálných částí vlastních hodnot linearizační matice. Vzhledem ke kvalitativní ekvivalenci linearizovaného systému a původního nelineárního systému v okolí hyperbolického bodu, musí tyto vlastní prostory představovat části obecnějších množin fázového prostoru, které obsahují všechny trajektorie mířící, resp. vycházející z hyperbolického bodu. Lze očekávat a dá se snadno ukázat, že tyto množiny jsou diferencovatelné variety stejné dimenze jako vlastní prostory linearizovaného systému. Navíc jsou vlastní prostory k těmto varietám v hyperbolickém bodě tečné, což vyplývá z definice linearizace a kvalitativní ekvivalence. Uvedené separatrix se nazývají stabilní a nestabilní variety a značí se obvykle E^s a E^u, kde s a u vyjadřuje dimenzi variety.

Poznámka:
V silněji nelineárních systémech může dojít k tomu, že se stabilní a nestabilní variety zakřiví tak, že se vzájemně dotknou a protnou. Z jejich charakteru vyplývá, že v místech průniku musí docházet ke složitým jevům, neboť trajektorie v této oblasti musí být stabilní i nestabilní zároveň. Skutečně je průnik variet-separatrix jedním z důležitých mechanizmů pro vznik chaotického chování, jak uvidíme v dalších kapitolách.