třídy podobnosti
kanonický tvar lineárních systémů
vlastní hodnoty
stabilní bod
nestabilní bod
sedlový bod
nepravý uzel
ohnisko
orbita
neregulární systém
globální analýza systému

3.1    Lineární systémy v rovině

Pokud je vektorová funkce F  lineární, lze psát soustavu (2.1) v maticovém tvaru

(3.1)

kde A je matice s konstantními koeficienty:

A =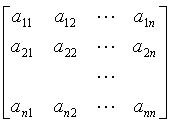

(3.2)

Při lineární transformaci stavových proměnných podle vztahu

(3.3)

kde M je regulární matice, lze přepsat soustavu (3.1) do tvaru

(3.4)

kde pro matici B platí

(3.5)

a matice B je tedy podobná s maticí A.

Všechny lineární soustavy (3.1) lze tedy rozdělit do několika tříd tak, že matice v jedné třídě spolu souvisí podle vztahu (3.5). Známe-li řešení soustavy v jedné třídě, pak řešení jiné soustavy z téže třídy dostaneme lineární transformací (3.3) nalezeného řešení.

3.1    Lineární systémy v rovině

Pro každé n existuje pouze konečný počet podobnostních tříd lineárních systémů s n stavovými proměnnými. Zde si shrneme pouze třídy lineárních systémů pro n=2 (fázovým prostorem je rovina).

Zástupce každé třídy se vyjadřuje v tzv. kanonické Jordanově formě a pro n=2 mají odpovídající matice J tvar:

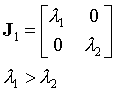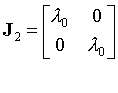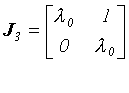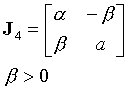(3.6)

Všechny koeficienty uvedených matic jsou reálná čísla.

Pro vlastní hodnoty l matic 2x2 platí obecný vztah plynoucí z definice

(3.7)

kde stopa matice je a determinant .

Vlastní hodnoty tedy nezávisí na všech koeficientech matice A, ale pouze na dvou výše uvedených parametrech.

Jednotlivé matice J se pak liší typem vlastních hodnot, které odpovídají různým typům kořenů uvedené kvadratické rovnice podle znaménka diskriminantu

• dvě reálné vlastní hodnoty: třída matic J₁ s vlastními hodnotami l₁, l₂,
• dvojnásobná vlastní hodnota: třída diagonálních matic J₂ s vlastní hodnotou l₀,
• dvojnásobná vlastní hodnota: třída nediagonálních matic J₃ s vlastní hodnotou l₀, neexistují dva lineárně nezávislé vlastní vektory,

• dvě komplexně sdružené vlastní hodnoty: třída matic J₄ s vlastními hodnotami a±ib.

Každý lineární dynamický systém popsaný vztahem (3.1) lze tedy vhodnou transformací (3.3) upravit na tvar

(3.8)

kde J je (v případě dvojrozměrného systému) matice jednoho z typů uvedených v (3.6).

Dá se očekávat, že fázový portrét uvedených kanonických systémů se pro různé třídy kvalitativně liší. Poddrobná analýza všech možností je jednoduchá a zároveň velmi instruktivní

Pro dvě různé reálné vlastní hodnoty je řešení soustavy (3.8) jednoduché:

(3.9)

Pro záporné vlastní hodnoty je systém stabilní, pro kladné nestabilní (viz obr.3.1). Stabilitou zde rozumíme konvergenci trajektorií systému s rostoucím časem do pevného bodu. Pokud je systém z tohoto stavu malou poruchou vychýlen, vrací se zpět. Na obr.3.1 vidíme, že všechny trajektorie vycházejí z počátku fázového prostoru, resp. všechny trajektorie se do tohoto bodu sbíhají. Počátek je v obou případech pevným bodem fázového prostoru, avšak v prvním případě je tento pevný bod nestabilní, neboť malá změna stavu způsobí nevratný pohyb systému.

Obr.3.1 Fázový portrét lineárního systému s reálnými a různými vlastními hodnotami:
l₁>l₂>0: nestabilní (vlevo)
l₂< l₁<0: stabilní (vpravo)

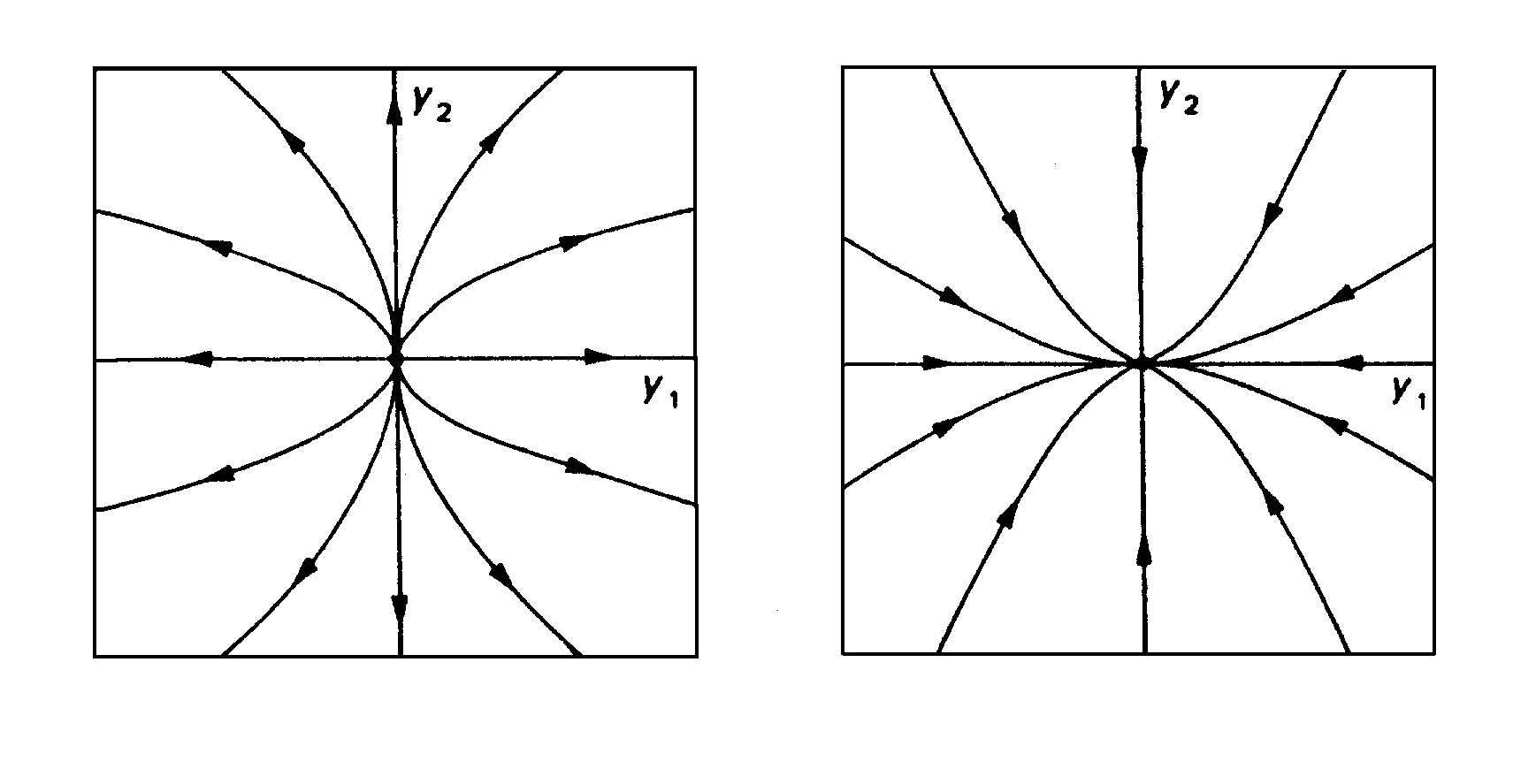
Pro reálné vlastní hodnoty s opačnými znaménky je fázový portrét odlišný: opět je v počátku fázového prostoru pevný bod, avšak pouze dvě trajektorie do něj vstupují a dvě (kolmé) vystupují. Uvedený typ bodu ve fázovém prostoru se nazývá sedlový.

Obr.3.2 Fázový portrét lineárního systému s vlastními hodnotami opačného znaménka (l₂<0<l₁). Systém obsahuje pevný bod v počátku, je nestabilní, pevný bod je sedlovým bodem.

Třída matic J₂

Z řešení soustavy s touto maticí ihned podle (3.9) vyplývá:

Fázový portrét systému (tzv. typ “hvězda”) s dvojnásobnou vlastní hodnotou je na obr.3.3. Pro zápornou vlastní hodnotu je systém stabilní, pro kladnou nestabilní.

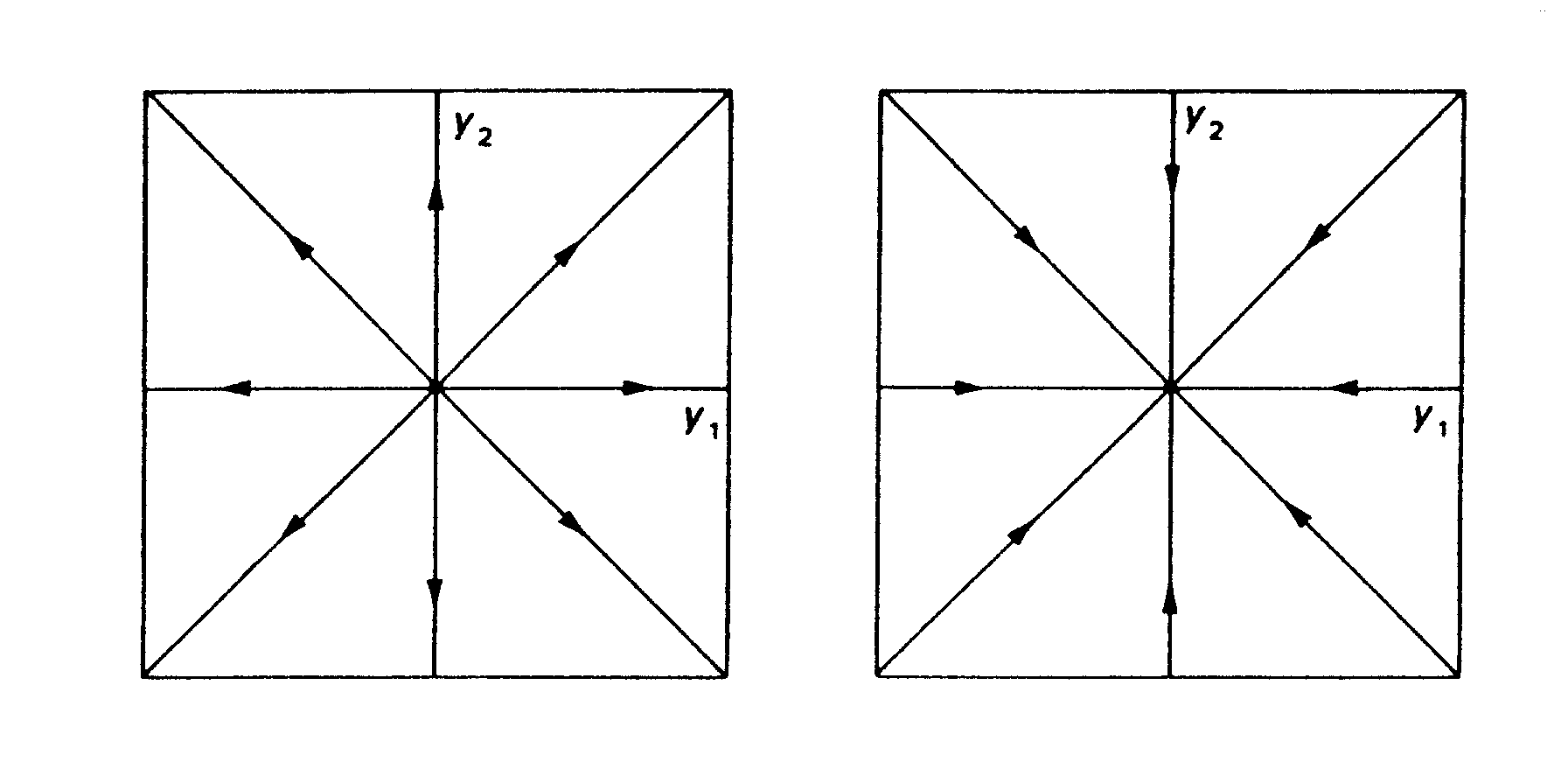
Obr.3.3 Fázový portrét diagonálního lineárního systému s dvojnásobnou vlastní hodnotou
l₀>0: nestabilní, l₀<0: stabilní.

Třída matic J₃

Pro nediagonální matici typu J₃ má systém (3.8) řešení:

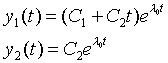(3.10)

Odpovídající fázový portrét je na obr.3.4. V počátku souřadnic je opět pevný bod, pro kladnou vlastní hodnotu nestabilní pro zápornou stabilní. Uvedený typ bodu se někdy nazývá nepravý uzel, neboť trajektorie do tohoto bodu směřují pod stejným úhlem.

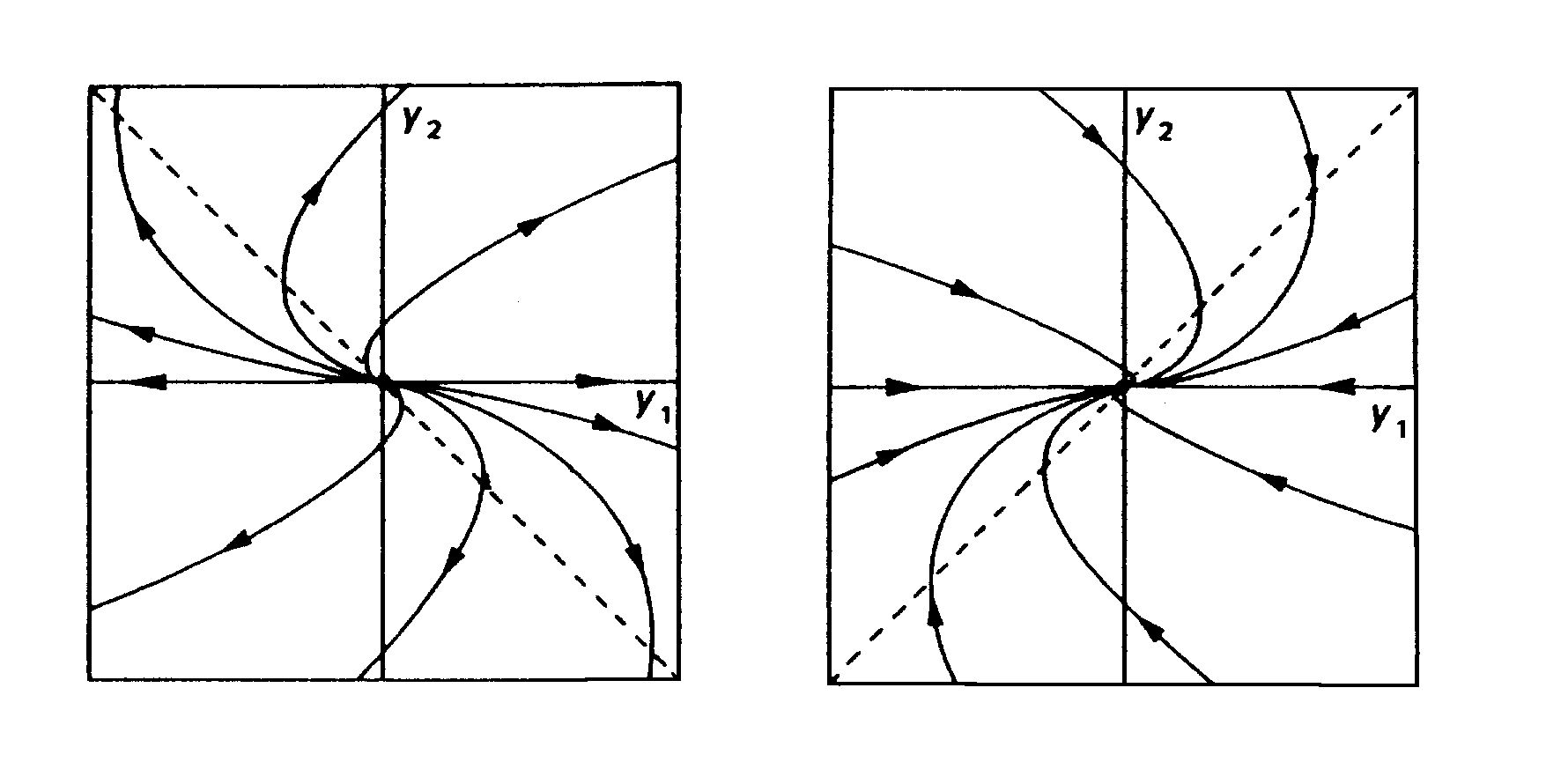
Obr.3.4 Fázový portrét nediagonálního lineárního systému

Třída matic J₄

Pro řešení kanonického systému s komplexními vlastními hodnotami se obvykle zavádí polární transformace souřadnic:

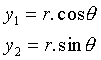(3.11)

Systém (3.8) pak přejde do tvaru

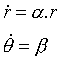(3.12)

s řešením

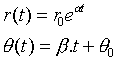(3.13)

Odpovídající fázové portréty jsou na obr.3.5. Pro a>0 tvoří trajektorie spirály vycházející z počátku fázového prostoru (pevný nestabilní bod, tzv. ohnisko). Pro a<0 je počátek stabilním ohniskem. Pro a = 0 tvoří trajektorie uzavřené křivky - orbity, pevný bod v počátku se nazývá střed (resp. centrum).

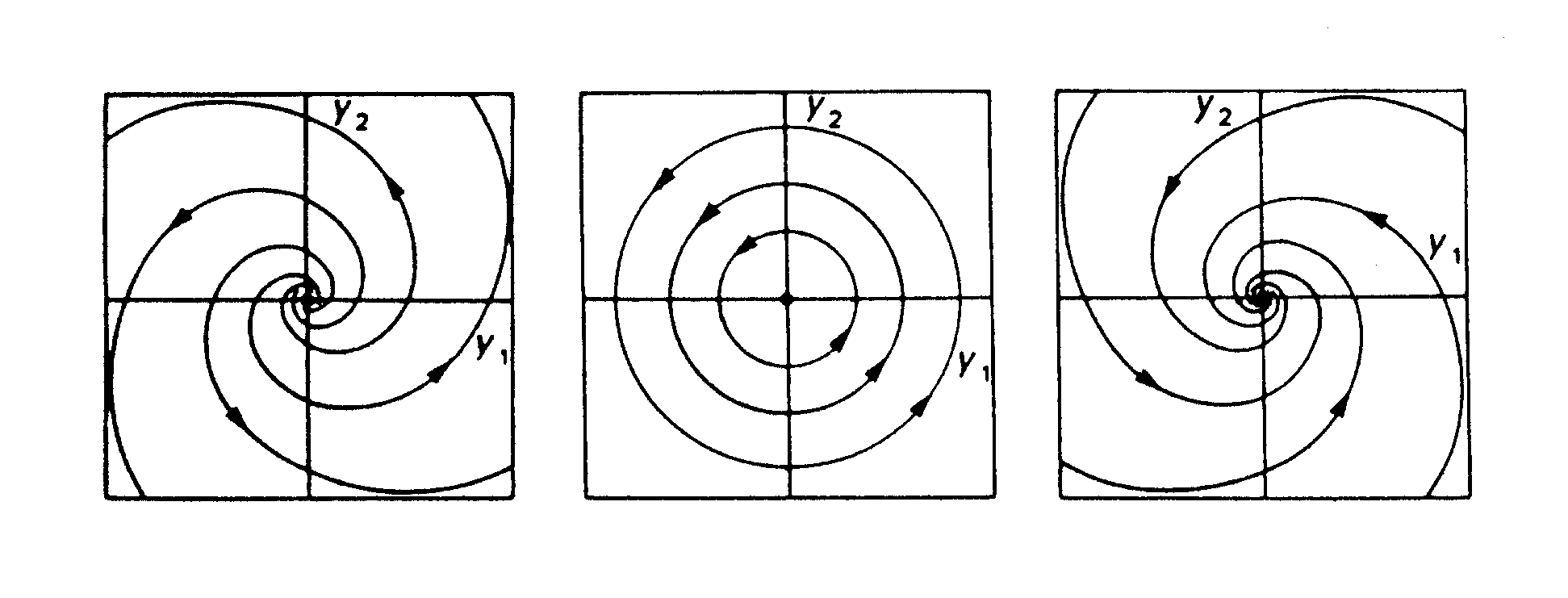
Obr.3.5 Fázový portrét lineárního systému s komplexními vlastními hodnotami.
a>0: nestabilní ohnisko, a=0: soustava soustředných orbit, a<0: stabilní ohnisko.

Kromě uvedených případů Jordanových matic, lze uvažovat ještě neregulární systémy (3.1) s neregulární maticí (det(A)=0), kdy existuje netriviální řešení rovnice Ax=0. Alespoň jedna z vlastních hodnot matice A je pak nulová, přičemž hodnost matice je 1 nebo 0. Odpovídající matice J jsou pak speciálními případy matic J₁ (l₂=0), resp. J₃ (l₀=0):

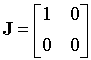, resp.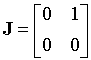

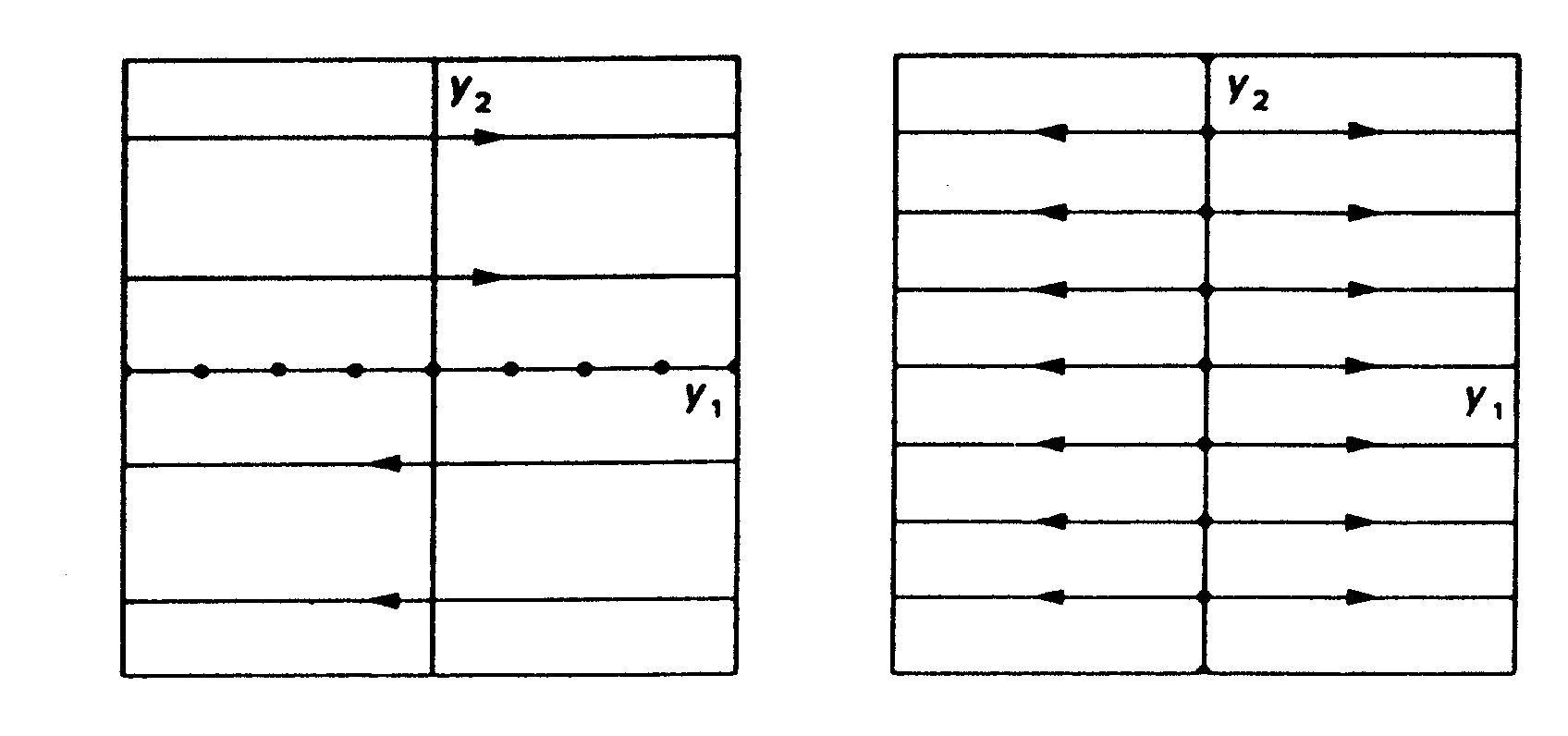
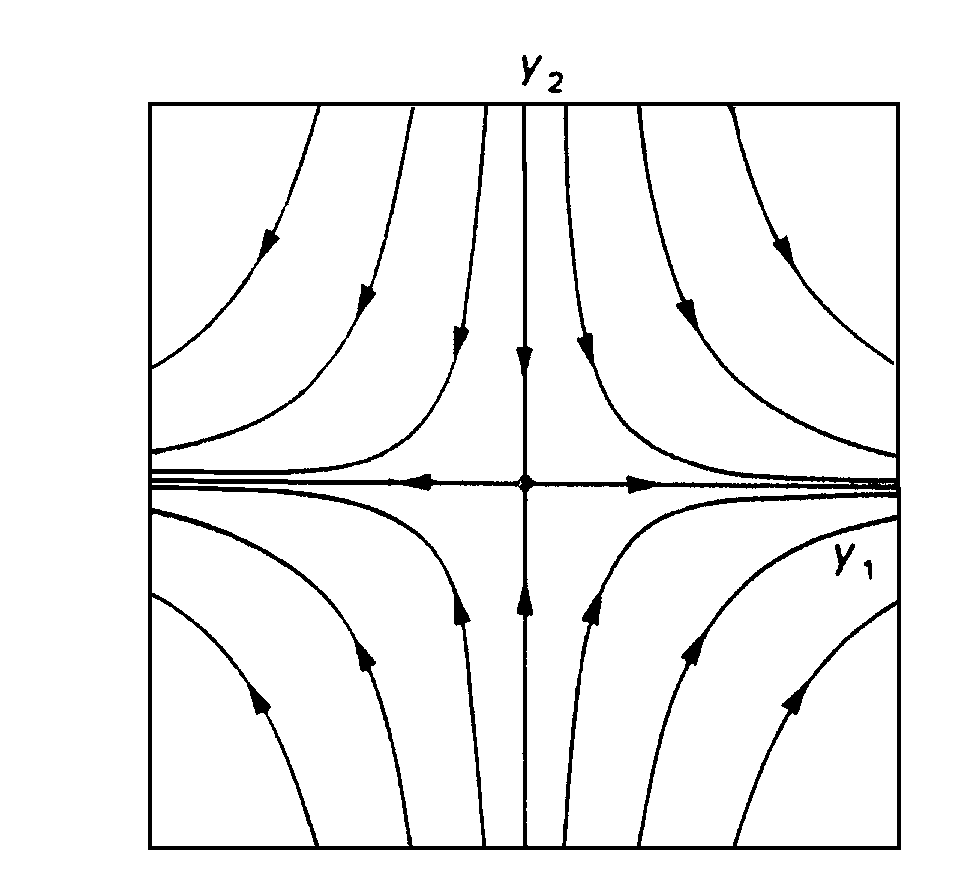
Obr.3.6 Fázový portrét lineárního systému s nulovou vlastní hodnotou.
Pro nediagonální matici představuje přímka y₂=0 množinu pevných stabilních bodů,
pro diagonální je přímka y₁=0 množinou pevných nestabilních bodů.

Poznámka:
Je-li matice lineárního dynamického systému nulová, je zřejmě každý bod fázového prostoru pevným bodem.

Celkovou situaci různých typů fázových portrétů ilustruje obr.3.7. Všechny lineární systémy lze rozdělit do tříd podle hodnot determinantu a stopy jejich matice koeficientů, neboť na nich závisí typ vlastních hodnot matice. Na obrázku nejsou zachyceny typy pro det(A)=0: v počátku souřadnic (matice A=0) je každý bod fázového prostoru stabilním bodem, vlevo a vpravo od počátku dostáváme fázové portréty podle obr.3.6.

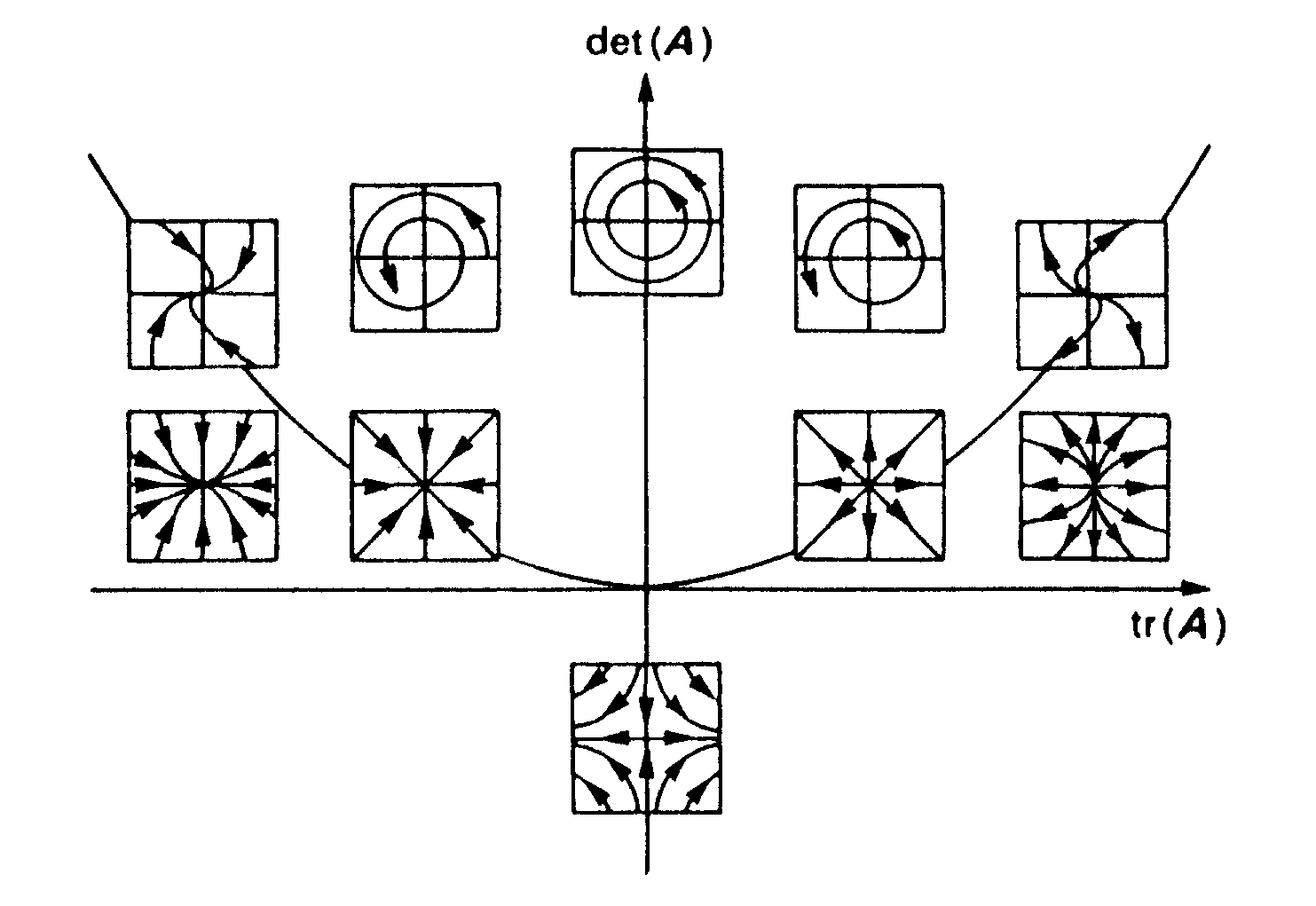
Obr.3.7 Rozdělení typů fázových portrétů podle matic koeficientů pro lineární systémy v rovině.