Simulace dynamických systémů v jazyce Java

6 Vícekomponentní systémy

Zajímavé možnosti pro hlubší pochopení fyzikálních dějů nabízí simulace konzervativních soustav sestávajících z mnoha vzájemně interagujících komponent. Nakonec, Poincarého pokusy o analýzu stability gravitačního systému ze začátku dvacátého století můžeme považovat ze počátek vyšetřování nelineárních jevů a první podložené reflexe paradoxů nelineárního světa.

V návrhu simulačního programu využijeme v maximální míře již získané znalosti, nová pro nás však bude zejména koncepce paralelní simulace více objektů tak, aby bylo možné za běhu programu jejich počet měnit. Tato dynamická vlastnost je užitečná nejen pro simulaci soustav s proměnným počtem prvků (např. dochází ke kreaci a anihilaci částic, resp. simulujeme velký kanonický systém), ale do jisté míry také zvyšuje přehlednost a správu objektů v soustavě.

Proměnný počet objektů naznačuje, že pro jejich uložení se nehodí datová struktura typu pole, která je vhodná spíše pro uložení dopředu známého počtu homogenních prvků. Místo toho se používají komplexnější datové struktury jako jsou vázané seznamy, kolekce, kontejnery objektů apod. Bohaté knihovny jazyka Java samozřejmě obsahují implementaci uvedených struktur, avšak my použijeme z didaktických důvodů vlastní jednoduchý návrh tak, aby byl nejen snadno pochopitelný, ale vzhledem k jednoduchosti i výpočetně nenáročný.

Navržená koncepce vychází z následujících předpokladů:

§ V soustavě komponent (např. částic) interaguje každá částice se všemi ostatními.

§ Uvažované interakce jsou aditivní, tj. výslednou sílu působící na částici lze je vyjádřit v podobě součtu příspěvků od ostatních částic. Na pořadí započítaných příspěvků nezáleží.

§ Interakce je symetrická (platí zákon akce a reakce).

V jednom simulačním kroku tedy vybereme částici, sečteme silová působení, kterými na ni působí všechny ostatních částice, a již známým postupem (např. klasickou metodou Runge–Kutta) nalezneme nový stav vybrané částice (a provedeme třeba její elementární animaci). Při sečítání příspěvků od jednotlivých částic nezáleží na pořadí, nepotřebujeme tedy přímý přístup ke všem částicím v soustavě. Postačí nám, když budeme schopni přejít od jedné částice k další tak, abychom sekvenčně prošli celou soustavu a nezapočetli žádnou částici vícekrát.

Symetrie interakce nám umožní celý algoritmu zkrátit na polovinu. Při přičítání silového působení libovolné jiné interagující částice na vybranou částici totiž můžeme zároveň s opačným znaménkem kumulovat sílu, kterou působí vybraná částice na tuto jinou částici.

6.1 Algoritmus výpočtu interakce v soustavě s proměnným počtem prvků

Pro uložení objektů použijeme jednoduchý lineární vázaný seznam, kdy každá částice obsahuje informaci o umístění následující. Pak musíme v soustavě udržovat informaci pouze o jediné (první) částici v seznamu, k ostatním se dostaneme zprostředkovaně. Že jsme vyčerpali všechny částice v soustavě (tj. dorazili na konec seznamu) poznáme podle toho, že poslední částice v seznamu informaci o další částici prostě neobsahuje.

Víme tedy, že každý objekt reprezentující částici v seznamu musí obsahovat ve formě atributů fyzikální vlastnosti částice (polohu, rychlost, hmotnost, …), ale také informaci o další částici v seznamu. Tato informace musí být co nejjednodušší, nechceme, aby jedna částice obsahovala v podobě atributu celý objekt jiné částice (tzv. vnořený objekt) – to je sice také možné, ale zcela neefektivní. V jazyce C bychom tuto informaci uložili ve formě tzv. ukazatele (určité reprezenatace adresy dalšího objektu v paměti). Takový atribut v podobě ukazatele zabírá pouze minimální místo v paměti a přístup k dalšímu objektu s jeho pomocí je velmi jednoduchý. Používání ukazatelů je v jazyce C (a C++) velmi frekventované – ukázalo se však, že s výhodami jdou ruku v ruce i značné nevýhody: programátor se tímto způsobem „přemísťuje v paměti“ značně nekontrolovaně a možné chyby v programu při používání ukazatelů jsou špatně odhalitelné a velmi zrádné.

Tento problém byl v jazyce Java elegantně odstraněn – o tom, zda informace o datech bude ve formě ukazatele, nebo se bude jednat o jiný mechanizmus (např. vnořený objekt), rozhoduje překladač jazyka sám. Zjednodušeně řečeno, pokud pracujeme s identifikátory objektů, používá Java vždy ukazatele. Tuto skutečnost si musíme důsledně uvědomovat při jejich používání – např. pokud pracujeme s identifikátorem objektA, který představuje nějaký objekt, a provedeme příkaz objektB = objektA, neznamená to, že identifikátor objektB bude obsahovat kopii objektu A. Ve skutečnosti bude pouze „ukazovat“ na tentýž objekt jako identifikátor objektA, tedy přiřazovacím příkazem se zkopíruje pouze „adresa“ objektu. Příkaz

objektB.atribut1=hodnota

pak způsobí, že tatáž hodnota bude výsledkem také výrazu objektA.atribut1.

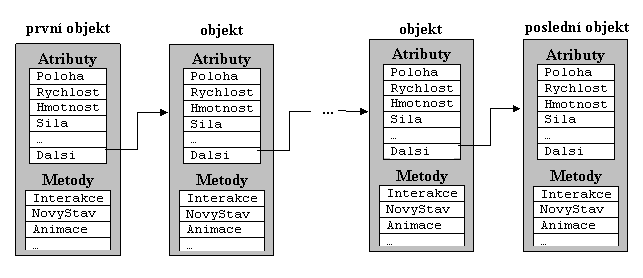
Obr. 6.1 Schema vázaného seznamu objektů interagujících částic

Slovně lze popsat algoritmus jednoho simulačního kroku v soustavě zhruba následovně:

Vezmeme první (referenční) částici A a počítáme silové účinky interakcí se všemi ostatními částicemi v seznamu. Ty pak kumulujeme v atributu částice sila. Po přičtení silového příspěvku od všech částic seznamu vypočteme nový stav referenční částice, neboť všechny parametry její pohybové rovnice již známe. Při výpočtu jednotlivých interakcí však v ostatních částicích také kumulujeme příspěvek od částice A. Pak prohlásíme za novou referenční částici další částici v seznamu, na kterou A ukazuje svým atributem dalsi a kumulujeme příspěvek od zbytku soustavy s výjimkou původní částice A, neboť její příspěvek již byl naplněn při výpočtu interakce prvků A a A.dalsi. Tímto způsobem se postupně stávají referenčními prvky všechny částice v seznamu, avšak výpočet interakce se zbytkem soustavy se neustále zkracuje. Poslední částice v seznamu v roli referenčního prvku již nemá v cyklu pro zbytek soustavy s kým interagovat (síla, která na ni působí, byla nakumulována při příležitosti procházení ostatních prvků), proto zde proběhne pouze výpočet nového stavu. Poslední prvek musí mít hodnotu atributu dalsi nastavenu na null (odpovídá ukazateli „nikam“). Přesněji pak celý postup popisuje vývojový diagram na obr. 6.2.

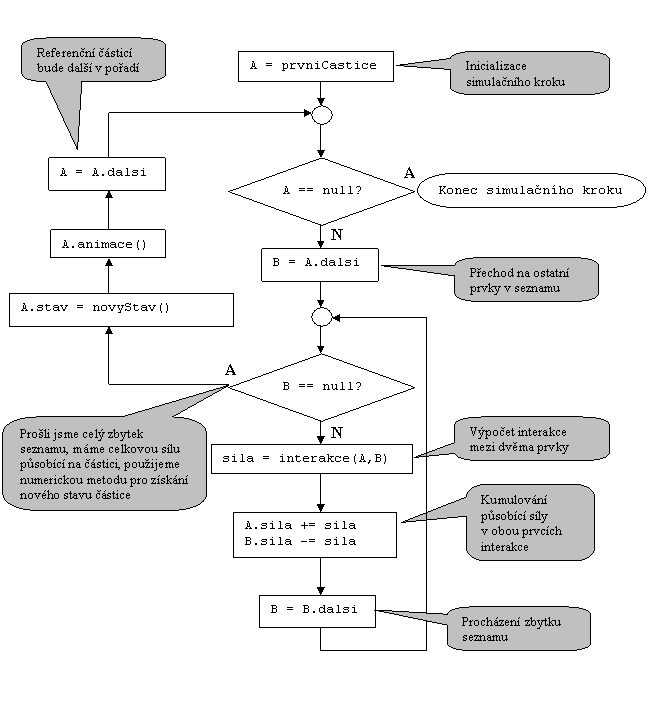
Obr. 6.2 Vývojový diagram simulačního kroku pro soustavu reprezentovanou vázaným seznamem

Návrh implementace třídy Soustava

Soustava částic bude představována objektem, který umožňuje globální pohled na celou soustavu. Jejím atributem bude zejmána první objekt vázaného seznamu, jehož prostřednictvím jsou přístupny i všechny ostatní částice. Dalším atributem může být počet prvků v soustavě.

Třída bude odvozena od vlákna tak, jako i v předcházejících případech. Případné zpomalení běhu budeme provádět pomocí veřejného atributu zpozdeni a vlákno ukončíme pomocí příznaku konec. Tělem vlákna bude cyklus opakování simulačních kroků.

Mezi metody objektu soustavy bude patřit zejména simulační krok naznačený na obr. 6.2. Soustava však musí disponovat funkcionalitou, která umožní dynamickou tvorbu vázaného seznamu – v nejjednodušším případě to zajistí metody přidání nového prvku do seznamu a odebrání vybraného prvku.

Velmi jednoduchá implementace třídy může vypadat např. takto:

class Soustava extends Thread

{

public int n;

public Castice prvni;

public boolean konec=false;

Soustava()

{

n = 0;

prvni=null;

}

public void pridej(Castice A) // přidá částici na začátek seznamu

{

if(n == 0)

první = A;

else

{

A.dalsi = prvni;

prvni = A;

}

n++;

}

public void odstran() // odstraní první částici ze soustavy

{

if(n > 0)

{

prvni = prvni.dalsi;

n--;

}

public void interakce(Castice A, Castice B) // implementace grav. interakce

{ // kumulujeme příspěvky zrychlení

double dx = B.x-A.x; // do obou interagujících částic

double dy = B.y-A.y; // pro simulaci jiné soustavy

double d2 = dx*dx+dy*dy; // s jiným typem interakce

double kd3 = 1/(d2*Math.sqrt(d2)); // postačí vyměnit tuto metodu

A.ax += B.m*kd3*dx; // grav. konstanta = 1

A.ay += B.m*kd3*dy;

B.ax -= A.m*kd3*dx;

B.ay -= A.m*kd3*dy;

}

public void krok() // metoda simulačního kroku

{

Castice A,B;

A = prvni;

while (A != null)

{

B = A.dalsi;

while (B != null)

{

interakce(A,B);

B = B.dalsi;

}

A.novyStav();

A = A.dalsi;

}

public void run() // tělo vlákna s vlastní simulací

{

while(!konec)

krok();

}

} // konec tridy Soustava

Třída má pouhé dva atributy – identifikátor první částice ve vázaném seznamu a počet částic v soustavě. Dokonce i druhý atribut je nadbytečný, protože počet prvků v seznamu lze jednoduchou metodou spočítat. Podle toho je i konstruktor třídy zcela triviální, třída je inicializována, jako prázdná, tj. neobsahující žádné částice.

Prvky do vázaného seznamu přidáváme metodou pridej(Castice A), přičemž musí být částice již vytvořena (viz dále třídu Castice). Částice je přidávána do neprázdného seznamu tak, že její atribut dalsi naplníme identifikátorem první částice a novou částici prohlásíme za první prvek seznamu.

Ještě snazší je odstranění první částice z neprázdného seznamu metodou odstran(). Identifikátor prvni identifikující první částici (ve skutečnosti ukazatel) naplníme hodnotou atributu prvni.dalsi, takže nyní ukazuje na druhý prvek v seznamu. Tím v programu zanikne jakýkoli identifikátor, kterým by byla původní první částice dostupná. Prostředí Javy se v takovém případě automaticky postará o odstranění objektu a uvolnění alokované paměti.

Mohlo by se zdát, že možnost přidání a odstranění pouze prvního prvku v seznamu je omezující. V našem případě interakce typu „každý s každým“ je však zcela postačující. V soustavě nám totiž nezáleží na tom, na jakou pozici v seznamu prvek přidáme (resp. odstraníme). Seznam nám pouze pomáhá procházet všechny objekty tak, abychom žádný nevynechali a žádný nezahrnuli vícekrát.

6.1.1 Gravitační soustava

Metoda gravitační interakce implementuje Newtonův vztah

kde k je gravitační konstanta, r₁₂ je vektor spojující těžiště obou částic, r⁰ je jednotkový vektor ve směru r₁₂. Je zřejmé, že pro složky zrychlení interagující částice lze psát

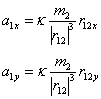což je použito v metodě interakce.

Metoda krok() přímočaře implementuje algoritmus popsaný vývojovým diagramem na obr. 6.2 a nevyžaduje komentář.

Tělo vlákna v metodě run() je popsáno v předcházejících příkladech.

Implementace třídy Castice

Objekt částice jsme zatím chápali pouze v abstraktním smyslu, vzhledem k významu se však podobá objektům, které jsme již používali: má atributy popisující jeho okaamžitý stav, konfigurační atributy (parametry) a metody, které při simulaci umožňují zejména nalézt nový stav objektu po časovém kroku.

class Castice

{

public double x,y,vx,vy,ax,ay; // stavové atributy

public double m,r; // parametry objektu

public Color color; // barva

public Castice dalsi; // atribut pro tvorbu vázaného seznamu

public Area area; // ukazatel na zobrazovací objekt

public int xold,yold,rold; // pomocné atributy pro animaci

// konstruktor naplní atriuty počátečními hodnotami

Castice(double x0, double y0, double vx0, double vy0,

double r0, int color0, Area area0)

{

x = x0; y = y0; r = r0; vx = vx0; vy = vy0;

m = r*r*r; // hmotnost nechť je úměrná objemu

ax = ay = 0;

color = new Color(color0);

dalsi = null; // nová částice není prvkem seznamu

xold = (int)x; yold = (int)y; rold = (int)r;

area = area0;

}

public void novyStav() // Eulerova metoda

{

x += simul.h*vx + 0.5*ax*simul.h*simul.h;

y += simul.h*vy + 0.5*ay*simul.h*simul.h;

vx += ax * simul.h;

vy += ay * simul.h;

ax = ay = 0; // nutné pro novou kumulaci příspěvků!!!

if(xold != (int)x || yold != (int)y) // animace jen v případě nutnosti

{ // kvůli zrychlení běhu

area.hide(xold,yold,rold);

// area.showLine(xold,yold,(int)x,(int)y,color); alternativní zobrazení

xold = (int)x; yold = (int)y;

area.show(xold,yold,rold,color);

}

} // konec třídy Castice

Implementace opět prakticky nevyžaduje komentář – konstruktor nastaví novému objektu počáteční hodnoty atributů a metoda novyStav() provede výpočet nového stavu a zároveň jednoduchou animaci objektu. Alternativní „vykomentovaná“ metoda showLine umožňuje zobrazování trajektorií místo animace (pochopitelně je nutné přesunout komentář na řádky s voláním animačních metod hide a show).

Pro výpočet nového stavu jsme kvůli jednoduchosti použili pouze modifikovanou Eulerovu metodu. Implementaci metody Runge-Kutta ponecháváme čtenáři. Úloha není úplně triviální, neboť si musíme uvědomit, že výpočet funkce ve vztahu (2.7) je třeba opakovat 4-krát, což, bohužel, znamená čtyřikrát opakovat metodu krok() podle algoritmu na obr. 6.2 s různými mezilehlými hodnotami. Nutno dodat, že gravitační úloha více těles je v případě jejich souměřitelných hmotností velmi nestabilní a použití klasické metody Runge-Kutta příliš nepomůže. V astronomické praxi se proto používají daleko sofistikovanější numerické metody vyšších řádů.

Objekt pro grafické znázorňení evoluce soustavy opět vychází z přístupu uvedeného v dřívějších kapitolách. Jeho metody umožňují skrýt a zobrazit částici, což je v podstatě vše, co potřebujeme.

class Area extends Canvas

{

public int width,height;

Area(int width0,int height0)

{

super();

width = width0; height = height0;

resize(width,height);

}

public void paint(Graphics g) //ovladač překreslení

{ //vytvoří pozadí

Rectangle r = this.bounds();

g.setColor(Color.black);

g.drawRect(0,0,r.width-1,r.height-1);

setBackground(Color.gray);

}

public void show(int x,int y,int r,Color color) // zobrazení částice

{ // v novém stavu

Graphics g = this.getGraphics();

g.setColor(color);

g.drawOval((int)(x-r),(int)(y-r),(int)r*2,(int)r*2);

}

public void hide(int x,int y,int r) // skrytí částice

{ // ve starém stavu

Graphics g = this.getGraphics();

g.setColor(Color.gray);

g.drawOval(x-r,y-r,r*2,r*2);

}

public void showLine(int x1,int y1,int x2,int y2,Color color)

{ // vykreslení trajektorie

Graphics g = this.getGraphics();

g.setColor(color);

g.drawLine(x1,y1,x2,y2);

}

Metoda showLine() umožňuje místo animovaného pohybu těles zobrazovat jejich prostorovou trajektorii. Oba typy zobrazení mohou být užitečné. Při animaci můžeme sledovat dynamiku vývoje soustavy – např. tělesa v „perihéliu“ se pohybují rychleji, dobře lze sledovat výměnu gravitační potenciální energie za kinetickou a naopak, zobrazení trajektorií dobře ilustruje celkovou složitost vývoje systému.

Implementace třídy simul

Stejně jako v ostatních případech potřebujeme hlavní třídu odvozenou od třídy Applet, která vytvoří všechny objekty a spustí vlastní simulaci. Kvůli jednoduchosti nastavíme všechny počáteční hodnoty simulované soustavy přímo v programu, prvky umožňují interaktivní zásahy do soustavy uživatelem zatím vynecháme. Třída simul tak bude obsahovat pouze krátký kód:

public class simul extends Applet

{

private Area area;

private Soustava soustava;

public static double h=0.00005; // diskretizační krok

public void init()

{

setLayout(new FlowLayout());

area = new Area(300,300);

add(area);

area.repaint();

soustava = new Soustava();

soustava.pridej(new Castice(150,250,-1.5,0,10,0x00FFFF,area));

soustava.pridej(new Castice(150,50,1.5,0,10,0xFFFF00,area));

soustava.pridej(new Castice(150,140,0,0,2,0xFFFFFF,area));

soustava.start();

}

public void stop()

{

soustava.konec = true;

super.stop();

}

Připomínáme, že vlákno soustavy je nutné spouštět prostřednictvím metody start(), zřejmý je postup vytvoření instance objektu soustavy a využití jejích metod pro přidání částic do soustavy. Je zde opět použit oblíbený postup vytvoření instance částice konstruktorem přímo v parametru metody, která s objektem dále pracuje.

Vzhledem k nestabilitě úlohy je třeba volit diskretizační krok značně malý (zde 5.10^-5, což vede k akceptovatelné rychlosti simulace u PC s jádrem procesoru alespoň 3 GHz), proto není vlákno zpožďováno metodou sleep, jako v předcházejících případech. Místo toho lze běh úlohy zpomalit dalším zmenšením diskretizačního kroku.

V našem případě jsme nastavili program na úlohu tří těles, kterou analyzoval již H. Poincaré. Dvě stejně hmotná tělesa obíhají kolem společného těžiště prakticky po kruhové dráze, třetí těleso má vůči nim téměř zanedbatelnou hmotnost (125:1). Dráha třetího tělesa je značně chaotická, je přitahována střídavě hmotnějšími tělesy, až se po relativně krátké době soustava rozpadne: málo hmotné těleso přejde na hyperbolickou dráhu a soustavu opustí, obě hmotná tělesa kompenzují vysokou kinetickou energii unikajícího tělesa snížením potenciální energie přechodem na nižší oběžnou dráhu.

Situaci ilustruje obrázek, který byl získán změnou animační metody na vykreslování trajektorií těles:

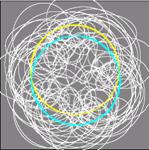Obr. 6.3 Záznam trajektorií tří těles podle uvedeného příkladu. Bílá trajektorie odpovídá tělesu s nízkou hmotností, žlutá a tyrkysová ilustrují pravidelné kuželosečky, které opisují dvě hmotná tělesa.

Je poměrně obtížné nastavit pro více těles počáteční podmínky tak, aby se soustava téměř ihned nerozpadla. Zajímavé je přidání čtvrtého tělesa identického s tělesem s nízkou hmotností, umístěného symetricky. Po relativně dlouhé regulérní fázi dojde ke spontánnímu narušení symetrie vlivem zaokrouhlovací chyby a rychlému rozpadu soustavy.

Uvedený program doplněný o interaktivní prvky nalezneme zde. Spusťte počáteční podmínky pomocí tlačítka Demo, pak zrychlete výpočet nastavením čekání vlákna na nulu v poli Delay[Enter].

Čtenář si snadno ověří nízkou numerickou stabilitu úlohy – vývoj trajektorií ze stejného počátečního stavu se rychle mění při změně diskretizačního kroku, nebo při náhradě numerické metody stabilnější metodou vyššího řádu. Vzhledem k tomu, že se jedná o konzervativní soustavu, můžeme si ověřit stabilitu metody sledováním celkové energie – integrálu pohybu.

Do objektu Castice přidáme atribut Ekin pro zaznamenání kinetické energie, která je vlastností tělesa. Při každé změně stavu můžeme vyjádřit kinetickou energii v metodě novyStav() takto:

Ekin = 0.5*m*(vx*vx+vy*vy);

Potenciální energie je vlastností soustavy, lokální potenciální energie zde nemá význam, proto musíme upravit objekt Soustava:

přidáme atributy pro celkovou kinetickou energii soustavy Ekin, celkovou potenciální energii Epot, a celkovou výslednou energii E, která by pochopitelně měla během simulace zůstávat konstantní.
do metody interakce(A,B) soustavy přidáme příkaz

Epot -= A.m*B.m*1/Math.sqrt(d2);

Připomínáme, že proměnná d2 obsahuje čtverec vzdálenosti těžišť (středů) částic, odečítání respektuje záporný charakter gravitačního potenciálu.

Nezapomeneme do metody krok() za volání A.novyStav() přidat kumulaci kinetické energie

Ekin += A.Ekin;

Na konci metody krok() bychom měli vyjádřit celkovou energii

E = Ekin + Epot;

a vynulovat atributy Ekin a Epot pro příští načítání příspěvků energií od částic a jejich interakcí.

Zobrazení průběhů energií již ponecháme na čtenáři. V nejjednodušší případě, kdy nám jde pouze o kontrolu správnosti simulace, lze numerickou hodnotu energie periodicky vypisovat na programovou konzoli např. příkazem

System.out.println("Celková energie: "+E);

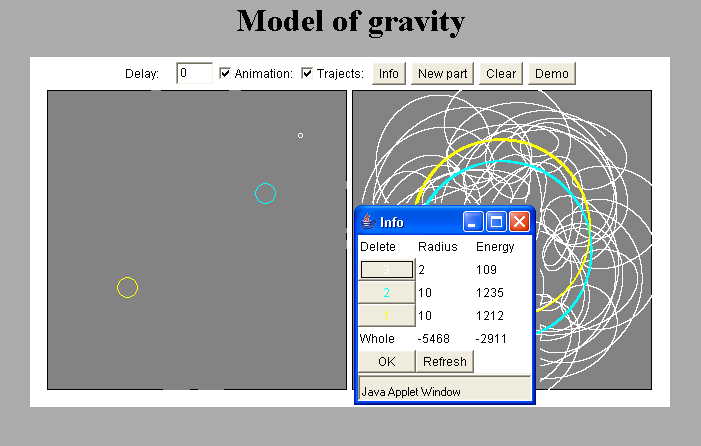Obr. 6.3a Příklad výše uvedeného programu doplněného o interaktivní prvky umožňují přidání částic v definovaném stavu a zobrazení informačního panelu s okamžitou hodnotou kinetické energie těles, celkovou konstantní energií soustavy (zde -2,9 kJ) a okamžitou hodnotou celkové potenciální energie, které musí být vždy záporná.

6.1.2 Pružný ráz koulí – ideální plyn

Gravitační interakce a pružné rázy (kontaktní interakce) představují velmi odlišné jevy, přesto je náš přístup k simulaci natolik univerzální, že umožňuje přechod od jedné soustavy ke druhé po pouze malé úpravě. Musíme si uvědomit, že navzdory faktu ojedinělých srážek, je nezbytné (stejně jako v případě permanentní interakce) v každém simulačním kroku volat metodu interakce typu „každý s každým“ – alespoň z toho důvodu, abychom se přesvědčili, že ke srážce nedošlo.

Metoda interakce tedy nejprve zjistí, zda poloha kruhových částic s ohledem na jejich rozměr nenaznačuje, že došlo ke srážce. Pokud nedošlo ke kontaktu, metoda nemění stav soustavy. V případě, že ke kontaktu došlo, metoda změní atributy vektoru rychlosti obou částic tak, aby byly respektovány okolnosti pružného rázu, tj. zákon zachování energie a zákon zachování hybnosti soustavy tvořené oběma interagujícícmi částicemi. V případě rovinné úlohy se jedná o tři vztahy, avšak změna rychlostí obou částic v rovině obsahuje čtyři neurčené hodnoty složek vektorů rychlosti. Čtvrtý (často opomíjený) vztah vyplývá z impulsu síly – interakce probíhá kontaktně, tj. nutně ve směru spojnice středů částic. Vektor změny hybnosti má tedy známý směr. Implementace interakce pak může vypadat např. takto:

public void interakce(Castice A, Castice B)

{

double k,deltaAvx,deltaAvy,deltaBvx,deltaBvy;

if((sqr(A.x-B.x)+sqr(A.y-B.y)) < sqr(A.r+B.r)) // test kolize

{

k=(A.x-B.x)/(A.y-B.y); // směr spojnice středů

deltaAvy=2*B.m/((A.m+B.m)*(k*k+1))*(B.vy-A.vy+k*(B.vx-A.vx));

deltaAvx=k*deltaAvy; // výpočet změny rychlostí

deltaBvx=-deltaAvx*A.m/B.m;

deltaBvy=-deltvaAvy*A.m/B.m;

A.vx+=deltaAvx; // oprava vektorů rychlostí

A.vy+=deltaAvy;

B.vx+=deltaBvx;

B.vy+=deltaBvy;

}

Odvození použitých vztahů je triviální a ponecháváme jej na čtenáři. Za zmínku stojí výpočet směrnice, kde není ošetřena možnost dělení nulou – interakce přesně v kolmém směru má sice pravděpodobnost takřka nulovou, avšak přísně vzato bychom měli ošetřit nejen tuto možnost, ale i stabilitu výpočtu tím, že bychom vybrali souřadný systém výpočtu tak, aby směrnice byla vždy menší než jedna.

Aby částice neopustily zobrazovanou plochu, musí se od jejích hranic rovněž pružné odrážet. Kromě metody Soustava.interakce je proto zapotřebí pozměnit také metodu novyStav v implementaci třídy Castice např. takto:

public void novyStav()

{

if ((0>(x-r))||(area.width<(x+r))) vx = -vx; // odraz od okrajů znamená

if ((0>(y-r))||(area.height<(y+r))) vy = -vy; // pouhou změnu znaménka

x += vx*simul.h; // vlastní změna stavu znamená

y += vy*simul.h; // rovnoměrný přímočarý pohyb

Ekin=0.5*m*(vx*vx+vy*vy); // kinetická energie částice

if (xold != (int)x | yold != (int)y)

{

if(show)

{

area.hidePart(xold,yold,rold);

// area.showLine(xold,yold,(int)x,(int)y,color);

xold=(int)x;yold=(int)y;

area.showPart(xold,yold,rold,color);

}

Metoda je rovněž zcela průhledná. Pokud si vybereme zobrazení trajektorií, dostaneme např následující obrázek:

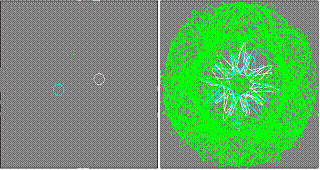
Obr. 6.4 Příklad vývoje soustavy s devíti tělesy s různou velikostí a hmotností – vlevo je animační zobrazení, vpravo trajektorie vývoje

Uvedený program doplněný o interaktivní prvky nalezneme zde. K dispozici je i možnost zobrazení rozdělení energií a jejich prvních statistických momentů pro ilustraci platnosti ekvipartičního principu.

Snadno se lze přesvědčit, že průměrná kinetická energie těles je již po krátkém běhu simulace prakticky stejná – platí ekvipartiční teorém. Vzhledem k různé hmotnosti částic to znamená, že lehčí částice se pohybují v průměru rychleji. Na soustavě si lze (překvapivě) ověřit i jiné zákonitosti termodynamiky jako je stavová rovnice, lineární závislost fluktucí energie na velikosti soustavy apod. Navzdory faktu, že se Boltzmannova statistická termodynamika opírá o zákony velkých čísel plynoucí z obrovského počtu částic v soustavě, vidíme, že skutečný původ nevratnosti – stěžejního faktu Boltzmannovy teorie – plyne z nelinearity, kterou do systému vnáší charakter pružného rázu. Je zajímavé, že platnost slavného Boltzmannova H–teorému, o který se termodynamika opírá, dodnes nebyla obecně dokázána ani pro případ slabší varianty, tzv. kvaziergodické hypotézy.

Na uvedené soustavě, která patrně jen velmi vzdáleně připomíná model jednoatomového plynu, lze provést mnoho dalších simulačních experimentů, které mají obecný charakter – od rovnovážného rozdělení rychlostí až po závislost střední volné dráhy, resp. střední doby mezi srážkami na energii soustavy, resp. na počtu částic apod.

Poznámka: interakce pružného rázu má úskalí v možné vysoké rychlosti částice při náhodném soustředění energie. Pro větší časový krok se pak může stát, že při testování kolize se částice nejen dotýkají, ale jsou částečně prolnuty. Pro řešení úlohy pružného rázu nemá tato okolnost význam, ale v našem algoritmu může nastat chyba: pokud budou výsledné rychlosti po řešení rázu takové, že se částice ani v dalším simulačním kroku neoddělí, bude jejich poloha vyhodnocena opět jako srážková a nové řešení rázu opět změní rychlost částic. Chyba se projeví kmitajícím svázáním částic. Možností, jak tento nedostatek opravit, je celá řada, jako velmi jednoduchou se jeví např. přidání atributu „stavu srážky“ do objektu částice. Ten se pak použije ve vyhodnocení interakce tak, že částice „ve stavu srážky“ jsou při řešení rázu ignorovány. „Stav srážky“ je metodou interakce nulován, jakmile se částice od sebe oddělí. Lze si však představit i sofistikovanější metodu, např. opravu stavu při kolizi nejen co se týče rychlostí, ale i polohy částic tak, aby se po kolizi přesně dotýkaly.

Obr. 6.4a Příklad programu s interaktivními prvky pro přidávání a odebírání částic ze soustavy. V tomto případě soustavu tvoří jedna velmi hmotná modrá částice, pět méně hmotných červených částic a 20 malých žlutých částic. Modrá částice vykonává v podstatě náhodnou procházku (Brownův pohyb), kterou lze ověřit „změřením“ platnosti Einsteinova vztahu. V informačním panelu vidíme, že střední kinetická energie částic je stejná pro všechny částice bez ohledu na jejich hmotnost, stejně tak vidíme, že střední kvadratická odchylka energie (první statistický moment) je u všech částic stejná. Ekvipartiční teorém patrně neplatí pouze pro střední hodnoty energie, ale i pro její statistické momenty.

6.1.3 Vázané oscilátory

Gravitační interakci lze v našem programu snadno změnit na elastickou. V tomto případě není zapotřebí v původním programu měnit nic, kromě typu interakce:

public void inter(Castice A, Castice B)

{

double dx = B.x - A.x;

double dy = B.y - A.y;

double d2 = dx*dx+dy*dy;

double r12 = Math.sqrt(d2);

double kd3 = k*(1-r0/r12);

A.ax = kd3*dx/A.m;

A.ay = kd3*dy/A.m;

B.ax = -kd3*dx/B.m;

B.ay = -kd3*dy/B.m;

Epot += k*(r0-r12)*(r0-r12)/2;

}

Předpokládáme, že částice jsou vázány lineární elastickou vazbou, kde proměnná r0 označuje rovnovážnou vzdálenost vazby a k její tuhost.

Obr. 6.5 Vývoj soustavy vázaných oscilátorů v rovině.

Třídu Castice můžeme použít z modelu pro gravitační interakci beze změn.

Uvedený model patrně nemá žádnou vazbu na fyzikální realitu, ale můžeme na něm opět dobře dokumentovat platnost ekvipartičního teorému – částice mají stejné průměrné hodnoty energie všech stupňů volnosti, tj. energie se rovnoměrně rozdělí také na potenciální a kinetickou část.

Uvedený obrázek 6.5 opět ilustruje soustavu s pouhými třemi částicemi – dvě jsou stejně hmotné, třetí částice má hmotnost o dva řády nižší. Ekvipartiční teorém má za následek vyšší rychlost lehké částice, která má proto úměrně delší trajektorii. Zajímavé je sledovat chaotickou změnu energie ve vazbě dvojice hmotnějších částic. Navzdory lineární elastické interakci se chová systém chaoticky vlivem prostorového uspořádání.

Uvedený program doplněný o interaktivní prvky opět nalezneme zde. Spusťte počáteční podmínky pomocí tlačítka Demo, pak zrychlete výpočet nastavením čekání vlákna na nulu v poli Delay[Enter].

6.1.4 Dvouatomový plyn

Pokusíme se nyní skloubit zkušenosti s elastickou interakcí a pružným rázem do soustavy „molekul“ z nichž každá obsahuje dvě částice („atomy“) spojené lineární pružnou vazbou. Je zřejmé, že prvky soustavy nyní představují molekuly, vytvoříme tedy co nejjednodušší třídu např. takto:

class Molekula

{

public Castice A; // odkazy na dva atomy tvořící molekulu

public Castice B;

public Molekula dalsi; // atribut pro vázaný seznam

public double r0 = 30; // rovnovážná délka vazby

public double k = 100; // tuhost elastické vazby

Molekula(Castice A0, Castice B0) // konstruktor vyžaduje dříve vytvořené atomy

{

A = A0;

B = B0;

dalsi = null; // zařazení do vázaného seznamu provádí Soustava

}

public void novyStav()

{

double dx = B.x-A.x; // výpočet vazebného zrychlení atomů

double dy = B.y-A.y; // na základě jejich vzdálenosti

double d2 = dx*dx+dy*dy;

double r12 = Math.sqrt(d2);

double kd3 = k*(1-r0/r12);

A.ax = kd3*dx/A.m;

A.ay = kd3*dy/A.m;

B.ax = -kd3*dx/B.m;

B.ay = -kd3*dy/B.m;

A.novyStav(); // volání nového stavu atomů

B.novyStav(); // na základě nastaveného zrychlení

}

Vidíme, že třída pro definici „molekuly“ je v podstatě triviální. Jejím jádrem je výpočet zrychlení obou „atomů“ molekuly na základě jejich vnitřní vazby. Fyzický přechod do nového stavu je obsažen přímo v atomech. Třídu pro definici atomu můžeme implementovat např. takto:

class Castice

{

public double x,y,vx,vy,ax,ay,m,r; // atributy stavu a fyzikálních vlastností

public Color color;

public Area area;

public int xold,yold,rold; // uložení starého stavu pro animaci

Castice(double x0, double y0, double vx0, double vy0, // konstruktor

double r0,int color0, Area area0)

{

x=x0; y=y0; r=r0; m=r*r; vx=vx0; vy=vy0; // inicializace atributů

color=new Color(color0);

xold=(int)x;yold=(int)y;rold=(int)r;

area=area0;

}

public void novyStav()

{

vx += ax*simul.h; // oprava rychlosti na základě vazebného zrychlení

vy += ay*simul.h;

if ((0>(x-r))||(area.width<(x+r))) vx = -vx; // odraz od okrajů

if ((0>(y-r))||(area.height<(y+r))) vy = -vy;

x += simul.h*vx + 0.5*ax*simul.h*simul.h; // oprava polohy

y += simul.h*vy + 0.5*ay*simul.h*simul.h; // pro zrychlený pohyb

if(xold!=(int)x | yold!=(int)y) // animace

{

area.hide(xold,yold,rold);

xold=(int)x;yold=(int)y;

area.show(xold,yold,rold,color);

}

Je zřejmé, že oproti implementaci při gravitační a elastické interakci zde přibyl pouze odraz částice od okrajů zobrazované plochy. Při výpočtu vždy aproximujeme v rámci časového kroku nový stav rovnoměrně zrychleným pohybem, kde rychlost je nastavena odrazem od hranic nebo kolizí s jinou částicí a zrychlení vazebnou interakcí definovanou ve třídě Molekula.

Další drobnou úpravu musíme provést ve třídě Soustava, neboť její prvky nyní netvoří přímo částice, ale molekuly. Proto musíme při interakci dvou molekul zkoumat možnost kolize každé částice z jedné molekuly s každou částicí z druhé molekuly. Vcelku se však jedná o drobnou a přímočarou úpravu, pro přehlednost zde však uvedeme celou definici třídy:

class Soustava extends Thread

{

public int n;

public Molekula prvni;

public boolean konec=false;

Soustava()

{

n = 0;

prvni=null;

}

public void pridej(Molekula A) // přidá molekulu na začátek seznamu

{

if(n == 0)

první = A;

else

{

A.dalsi = prvni;

prvni = A;

}

n++;

}

public void odstran() // odstraní první molekulu ze soustavy

{

if(n > 0)

{

prvni = prvni.dalsi;

n--;

}

public void kolize(Castice A, Castice B)

{

double k,deltaAvx,deltaAvy,deltaBvx,deltaBvy;

if((sqr(A.x-B.x)+sqr(A.y-B.y)) < sqr(A.r+B.r)) // test kolize

{

k=(A.x-B.x)/(A.y-B.y); // směr spojnice středů

deltaAvy=2*B.m/((A.m+B.m)*(k*k+1))*(B.vy-A.vy+k*(B.vx-A.vx));

deltaAvx=k*deltaAvy; // výpočet změny rychlostí

deltaBvx=-deltaAvx*A.m/B.m;

deltaBvy=-deltvaAvy*A.m/B.m;

A.vx+=deltaAvx; // oprava vektorů rychlostí

A.vy+=deltaAvy;

B.vx+=deltaBvx;

B.vy+=deltaBvy;

}

public void interakce(Molekula A, Molekula B) // interakce molekul

{ // zkoumá srážky

Interakce(A.A,B.A); // jednotlivých atomů

Interakce(A.B,B.A);

Interakce(A.A,B.B);

Interakce(A.B,B.B);

}

public void krok() // metoda simulačního kroku

{

Molekula A,B;

A = prvni;

while (A != null)

{

B = A.dalsi;

while (B != null)

{

interakce(A,B);

B = B.dalsi;

}

A.novyStav();

A = A.dalsi;

}

public void run() // tělo vlákna s vlastní simulací

{

while(!konec)

krok();

}

} // konec tridy Soustava

Proti předcházející verzi jsme tedy všude zaměnili objektový typ Castice za typ Molekula, přidali pomocnou metodu pro kolizi částic, kterou jsme převzali z úlohy o pružném rázu, a konečně implementovali novou metody interakce, která pouze volá metodu kolize pro různé permutace částic v interagujících molekulách.

Nakonec je zapotřebí správně nastavit počáteční podmínky v konstruktoru třídy simul např. takto:

public void init() // konstruktor appletu

{

setLayout(new FlowLayout());

area = new Area(300,300);

add(area);

area.repaint();

soustava = new Soustava();

soustava.pridej(new Molekula(new Castice(150,150,1,0,10,0x00FFFF,area),

new Castice(150,180,1,0,10,0x00FFFF,area));

soustava.pridej(new Molekula(new Castice(100,150,1,0,10,0x0000FF,area),

new Castice(100,180,1,0,10,0x0000FF,area));

soustava.pridej(new Molekula(new Castice(200,150,1,0,10,0x00FF00,area),

new Castice(200,180,1,0,10,0x00FF00,area));

soustava.start();

}

Opět je použit konstruktor přímo v parametru metody (dokonce vnořený). Tento způsob umožňuje nevytvářet zbytečné identifikátory, které stejně nebudou nikde použity. Soustava nyní obsahuje tři molekuly s identickými atomy.

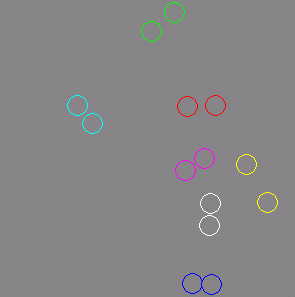Obr. 6.6 Příklad animace sedmi molekul. Kvůli použití modifikované Eulerovy metody musíme nastavit malý časový krok (zde 5.10^-5). I tak je však rychlost simulace rozumná.

Uvedený program doplněný o interaktivní prvky opět nalezneme zde. Nejprve vložte částici, pak zrychlete výpočet nastavením čekání vlákna na nulu v příznaku Slow.

Zajímavá je skutečnost, že každá molekula má pět stupňů volnosti (dva pro pohyb těžiště v rovině, rotační, vazebný a kinetický vyjadřující pohyb atomů relativně k těžišti soustavy). Energie každého stupně volnosti lze sečítat, jak již bylo ukázáno dříve, a ověřit platnost ekvipartičního teorému, který zpětně prokáže skutečně pět stupňů volnosti. Zmiňujeme se o tom zejména proto, že je zažitá představa, že vnitřní vazby snižují počet stupňů volnosti. Platí to však jen pro tuhou vazbu. V případě elastické vazby máme naopak o jeden stupeň volnosti víc. V tomto modelu platí ekvipartiční teorém v širokém spektru počátečních podmínek i pro jedinou molekulu v soustavě. Po každém nárazu na stěny se molekula roztočí a kmitá jiným způsobem, což postačuje ke statistickému vyrovnání. Opět vidíme, že platí zákony statistické fyziky, které nejsou důsledkem zákona velkých čísel, ale přítomností nelinearity.

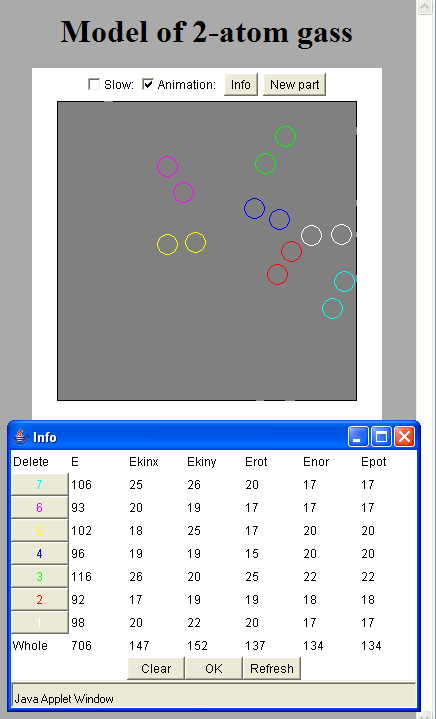Obr. 6.6a Program doplněný o interaktivní prvky a informační panel s rozdělením energií na jednotlivé stupně volnosti. Po krátkém běhu simulace (nejlépe s vypnutým zobrazováním) se průměrné energie molekul rovnoměrně rozdělí podle ekvipartičního teorému na posuvné, rotační a potenciální složky.

Obsah